A particle of mass 1kg has velocity v1=(2t)ˆi and another particle of mass 2kg has velocity v2=(t2ˆj.
Match the following columns.
Column1Column2A Net force on center of mass at 2sP209unitB Velocity of center of mass at 2sQ√68unitC Displacement of center of mass in 2sR√80/3unit-(S None
The correct Answer is:(A) → q; (B) → r; (C ) → p
For 1kgv1=(2t)ˆj=4ˆi,a1=2ˆi=2ˆi
for 2kgv2=t2ˆj=4ˆj,a2=2tˆj=4ˆj
(A) Acceleration of centre of mass =m1a1+m2a2m1+m2
→acm=23ˆi+83ˆj⇒acm=√49+649⇒√683m/s2
f=macm=√68N
(B) Velocity of centre of mass
→vcm=m1v1+m2v2m1+m2=(43ˆi+83ˆj)m/s
⇒|→vcm|=√169+649⇒√803
(C ) →vcm=1(2t)ˆi+2(t2ˆj)1+2+23tˆi+23t2ˆj
Displacement =∫20→vcmdt=[32(t22)2ˆi+23(t33)ˆj]20=43ˆi+169ˆj
⇒|Dispalcement|=√(43)2+(169)2=209 unit
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B14videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II43videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A particle of mass 1kg has velocity →v1=(2t)ˆi and another particle of mass 2kg has velocity →v2=(t2)ˆj
Column IColumn II(A)Netforce on centre of mass at 2 s(p)209unit(B)Velocity of centre of mass at 2 s(q)√68 unit(C)Displacement of centre of mass in 2s(r)√803unit(s)NoneView SolutionA particle of mass 1 kg is projected upwards with velocity 60ms−1. Another particle of mass 2kg is just dropped from a certain height. After 2s, match the following.
[Take, g =10ms−2]
column1column2Accelertion of CMP ZeroB Velocity of CMQ 10 SI unitC Displacement of CMR 20 SI unit-S NoneView Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 1 g moving with a velocity →v1=3ˆi−2ˆjms−1 experiences a perfectly in elastic collision with another particle of mass 2 g and velocity →v2=4ˆj−6ˆkms−1. The velocity of the particle is
A2.3ms−1B4.6ms−1C9.2ms−1D6ms−1
Four point masses are placede at four corners of a square of side 4m as shown. Match the following columns.

Column1Column2A x-coordinate of center of mass of 4kg and 2kgP (7//2)mB x-coordinates of center of mass of 4kg 2kg and 3kgQ (4//3)mC y-coordinate of center of mass of 1kg 4kg and 3kgR 3my-coordinate of center of mass of 1kg and 3kg(20/9)mView SolutionIn a two block system in figure match the following.
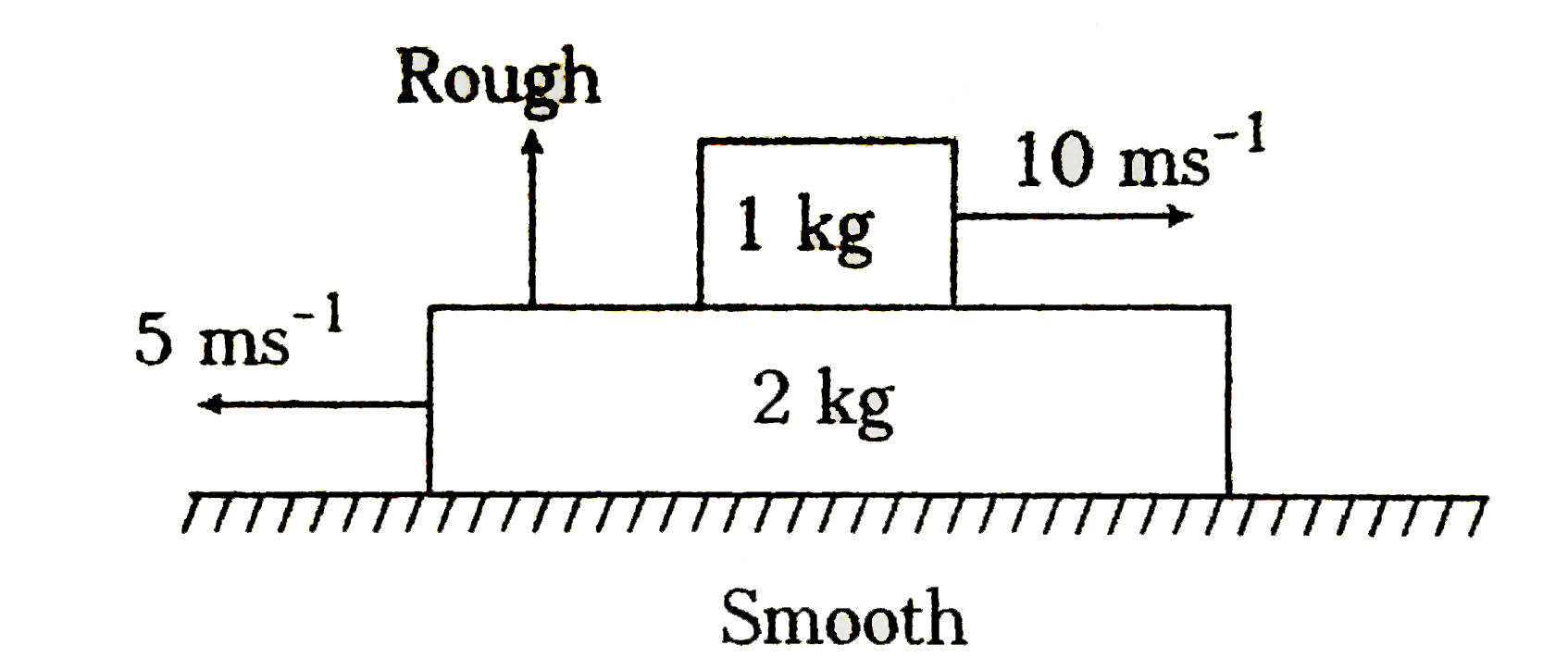 Column1Column2A Velocity of center of massP Keep on changing all the timeB Momentum of center of massQ First decreases then become zeroC Momentum of 1kg blockR ZeroD Kinetic energy of 2kg blockS ConstantView Solution
Column1Column2A Velocity of center of massP Keep on changing all the timeB Momentum of center of massQ First decreases then become zeroC Momentum of 1kg blockR ZeroD Kinetic energy of 2kg blockS ConstantView SolutionTwo particles of equal mass have coordinates (2m,4m,6m) and (6m,2m,8m). Of these one particle has a velocity v1=(2i)ms−1 and another particle has a velocity v2=(2j)ms−1 at time t=0. The coordinate of their center of mass at time t=1s will be
View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
 View Solution
View SolutionIn the diagram shown in figure, match the following columns (take g=10ms−2)

Column IColumn II(A) Normal reaction(p) 12 SI unit(B) Force of friction(q) 20 SI unit(C) Acceleration of block(r) zero(s) 2 SI unitView SolutionIn the arrangement shown in figure match the following
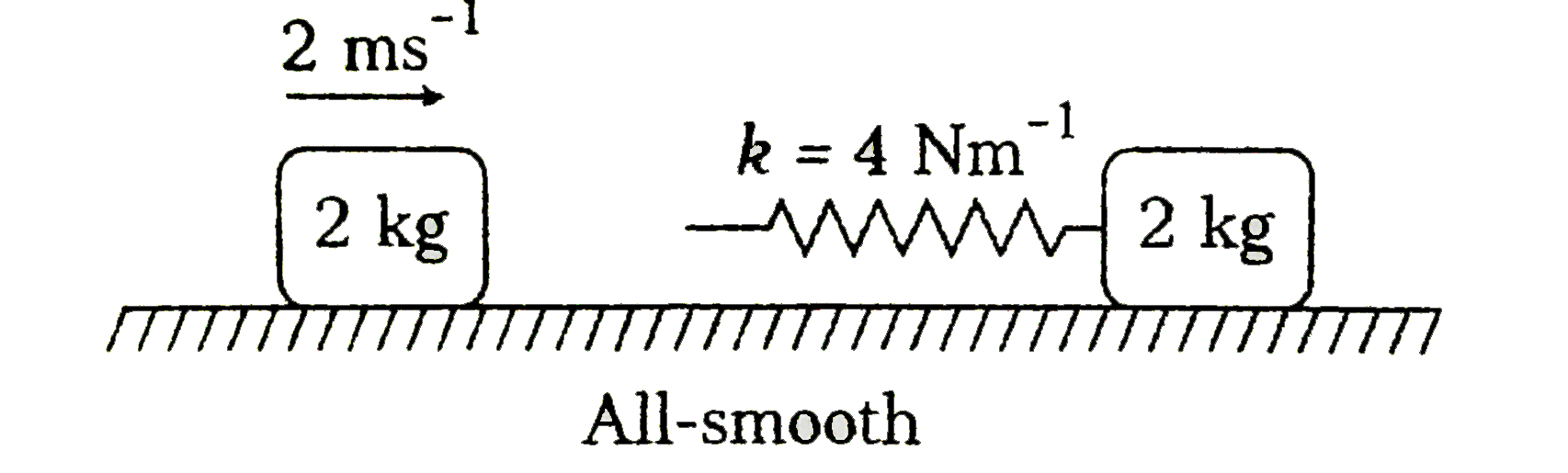
column1column2A Velocities of center of massP 2SI unitB Velocity of combined mass when compression in the spring is maximumQ 1 SI unitC Maximum compression in the springR 4 SIunitD Maximum potential energy stored in the springS 0.5SI unitView SolutionA particle of mass 2kg is moving with velocity →v0=(2ˆi−3ˆj)m/s in free space. Find its velocity 3s after a constant force →F=(3ˆi+4ˆj)N starts acting on it.
View Solution

