Vessel A contains an ideal gas at a pressure 5×105 Pa and is connected with a heat source which maintains its temperature at 300K. Another vessel B which has four time greater inner volume contains the same gas at a pressure 105 Pa and is connected to a heat source which maintains its temperature at 400K. What will be the pressure of entire system if two vessels are connected by a narrow tube tap:-
105Pa
2×105Pa
4×105Pa
5×105Pa
The correct Answer is:B
To solve the problem, we need to find the pressure of the entire system when vessels A and B are connected. Let's break it down step by step.
Step 1: Identify the given values
- For vessel A:
- Pressure, PA=5×105Pa
- Temperature, TA=300K
- Volume, VA=V (let's denote the volume of vessel A as V)
- For vessel B:
- Pressure, PB=105Pa
- Temperature, TB=400K
- Volume, VB=4V (since it has four times greater inner volume)
Step 2: Calculate the number of moles in each vessel
Using the ideal gas law, the number of moles N can be calculated as:
N=PVRT
For vessel A:
NA=PAVARTA=(5×105)VR×300
For vessel B:
NB=PBVBRTB=(105)(4V)R×400
Step 3: Simplify the expressions for NA and NB
Substituting the values:
NA=(5×105)V300R
NB=(105)(4V)400R=(105)(4V)400R=(105)(V)100R=(105)V100R=(105)V100R=(105)V100R=(105)V100R=(105)V100R
Step 4: Total number of moles in the system
The total number of moles N in the system is:
N=NA+NB=(5×105)V300R+(105)V100R
Step 5: Find the new pressure when the vessels are connected
When the two vessels are connected, the pressure in both vessels will equalize. Let P′ be the final pressure in the system. The total number of moles can also be expressed as:
N=P′(VA+VB)RT′
Where T′ is the effective temperature of the system.
Step 6: Set up the equation for pressure
Equating the two expressions for N:
(5×105)V300R+(105)V100R=P′(V+4V)RT′
Step 7: Solve for P′
Substituting TA and TB:
P′=(5×105)V300R+(105)V100R⋅R(TA+4TB)5V
Step 8: Substitute values and simplify
Substituting TA=300 K and TB=400 K:
P′=(5×105)V300R+(105)V100R⋅R(300+4⋅400)5V
Step 9: Final Calculation
After simplifying, we find:
P′=2×105Pa
Final Answer
The pressure of the entire system when the vessels are connected is:
P′=2×105Pa
- For vessel A:
- Pressure, PA=5×105Pa
- Temperature, TA=300K
- Volume, VA=V (let's denote the volume of vessel A as V)
- Pressure, PB=105Pa
- Temperature, TB=400K
- Volume, VB=4V (since it has four times greater inner volume)
Using the ideal gas law, the number of moles N can be calculated as:
N=PVRT
NA=PAVARTA=(5×105)VR×300
NB=PBVBRTB=(105)(4V)R×400
Substituting the values:
NA=(5×105)V300R
NB=(105)(4V)400R=(105)(4V)400R=(105)(V)100R=(105)V100R=(105)V100R=(105)V100R=(105)V100R=(105)V100R
The total number of moles N in the system is:
N=NA+NB=(5×105)V300R+(105)V100R
When the two vessels are connected, the pressure in both vessels will equalize. Let P′ be the final pressure in the system. The total number of moles can also be expressed as:
N=P′(VA+VB)RT′
Where T′ is the effective temperature of the system.
Equating the two expressions for N:
(5×105)V300R+(105)V100R=P′(V+4V)RT′
Substituting TA and TB:
P′=(5×105)V300R+(105)V100R⋅R(TA+4TB)5V
Substituting TA=300 K and TB=400 K:
P′=(5×105)V300R+(105)V100R⋅R(300+4⋅400)5V
After simplifying, we find:
P′=2×105Pa
The pressure of the entire system when the vessels are connected is:
P′=2×105Pa
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
71 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3
99 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A closed vessel 10L in volume contains a diatomic gas under a pressure of 105N/m2. What amount of heat should be imparted to the gas to increase the pressure in the vessel five times?
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
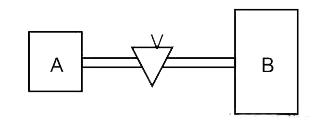
The valve V is adjusted to allow the pressure to equalize, but the temperature of each container is kept constant at the initial value, then the pressure in the two containers is :
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
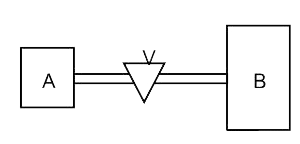
Before the valve V is opened, the ratio of number of moles of gas in A and B is :
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
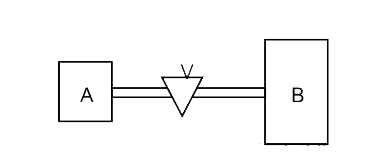
Before the valve V is opened, VA and VB are rms velocities of the molecules in container A and B then VAVB is:
View SolutionTwo spherical vessel of equal volume are connected by a n arrow tube. The apparatus contains an ideal gas at one atmosphere and 300K. Now if one vessel is immersed in a bath of constant temperature 600K and the other in a bath of constant temperature 300K. then the common pressure will be
View SolutionA vessel of volume 0.2m3 contains hydrogen gas at temperature 300 K and pressure 1 bar. Find the heat required to raise the temperature to 400 K. The molar heat capacity of hydrogen at constant volume is 5cal/molK.
View SolutionThe volume of a certain mass of gas at a pressure of 5×104Pa is doubled adiabatically. What is the final pressure of the gas ? [γ=1.4]
View SolutionA closed vessel of volume 0.2m3 contain hydrogen gas at temperature 300K and pressure 105Pa. Then the heat required to raise temperature to 600K is:(molar heat capacity of hydrogen at constant volume is 5cal/mol−K)
View SolutionA vessel of capacity 400cm3 contains hydrogen gas at 1 atm pressure at 7∘C. In order to expel 28.57cm3 of the gas at the same pressure, to what temperature the vessel should be heated ?
View SolutionA cylinder contains gas at 2×105Paand 47∘C. The cylinder is steadily heated. Neglecting any change in its volume, find the temperature at which the cylinder will break if the walls of cylinder can bear a maximum pressure of 8×105Pa
View Solution
