Question

A small marble of mass m moves in a circular orbit very close to the bottom of a circular bowl. Assume that the marble can only move in orbits whose angular momentum is $L=\frac{nh}{2\pi }$ where h is plank constant.

Options

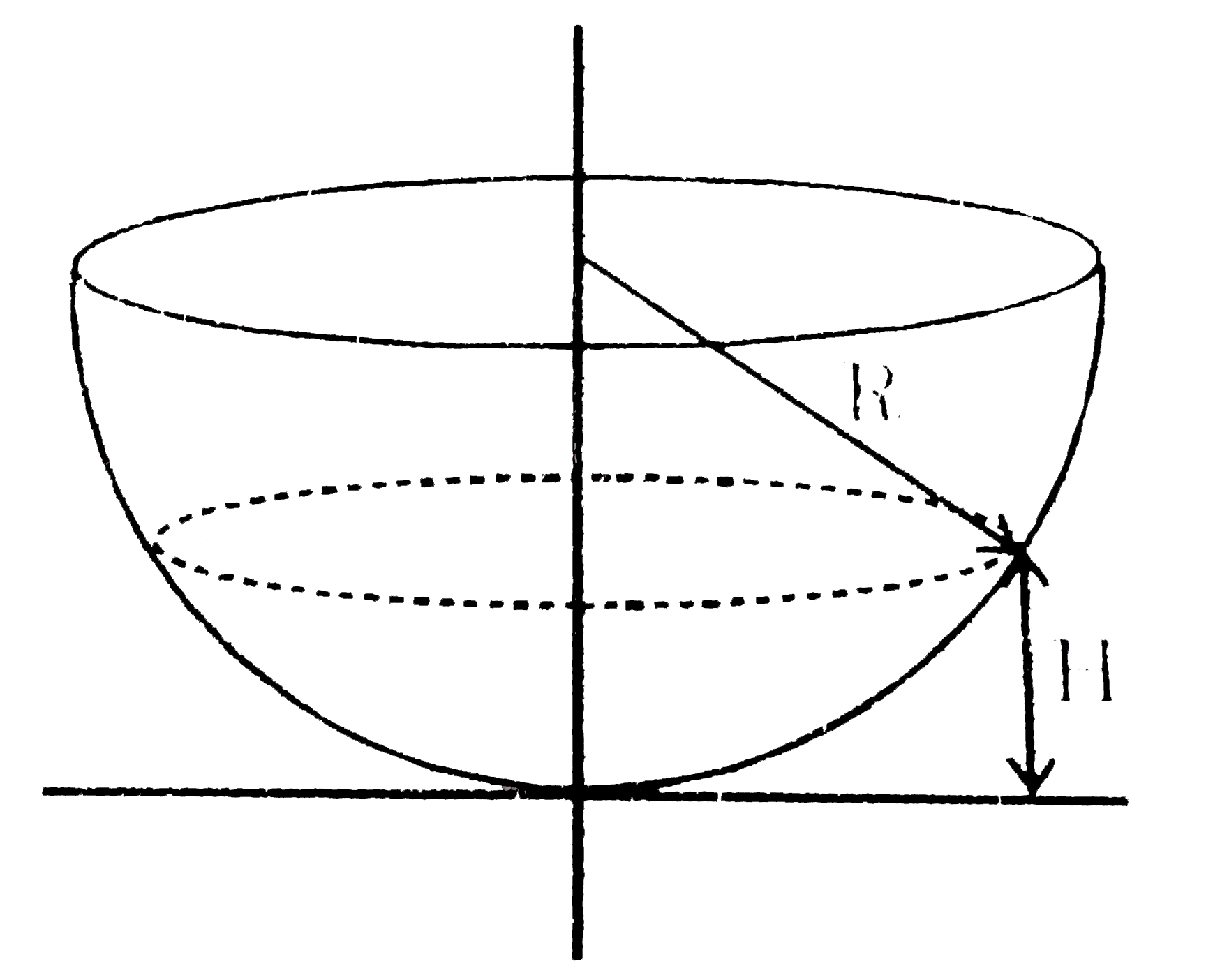
A. a.The allowed radius of the circular orbit is proportionsl to `n(3//2)`
B. b. The allowed speed is proportional to `n(1//2)`
C. c, Taking gravitional potential energy at bottom to be zero, the allowed energy is given by `(nh)/(2pi) sqrt((g)/(R )`
D. d.Gravotational potential energy and kinetic energy in any allowed state are equal (taking reference at bottom.)

Answer

B::C::D

Explanation

`Ncostheta = mg`
`N sin theta = (mv^(2))/(x)`

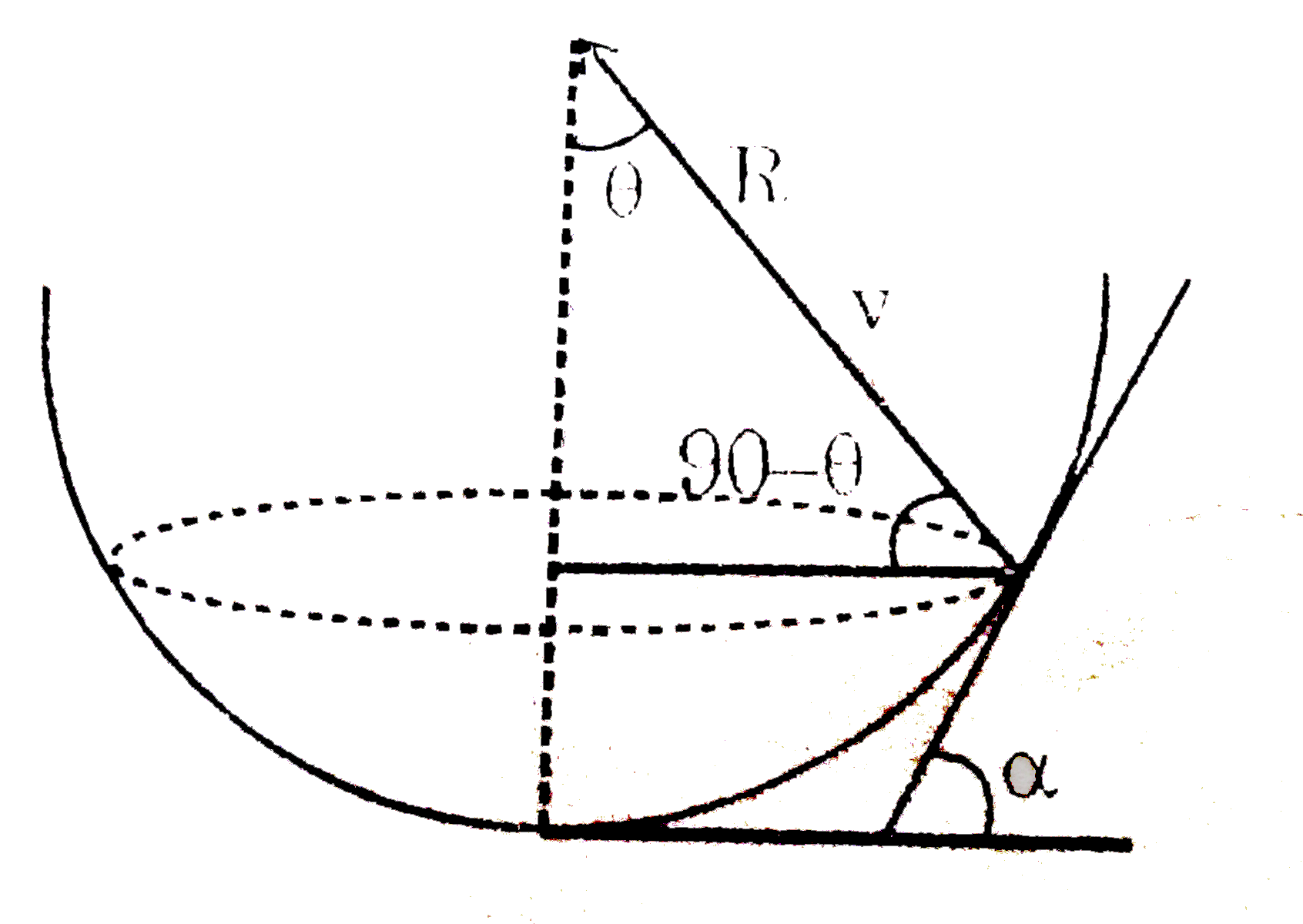
` tan theta=(v^(2))/(gx)=(v^(2))/(gR sin theta)`
`mvx = (nh)/(2pi)`
`mvxx R sin theta = (nh)/(2pi)`
`m sqrt((gR sin ^(2) theta)/(cos theta)) R sin theta = (nh)/(2pi)`
`m sqrt(gR^(3)) (sin^(2)theta)/sqrt(costheta) = (nh)/(2pi)`
`cos theta ~~1`
`m sqrt(gR^(3))xx(x^(2))/(R^(2))=(nh)/(2pi)`
`x=sqrt((nh)/(2pim)sqrt((R )/(g)))`
`v prop sqrt(n)`
`v = sqrt(nh)/(sqrt(2pisqrt(m)))xxsqrt((nh)/(2pim)sqrt((R)/(g)))=sqrt((nh)/(2pim)sqrt((g)/(R)))`
`E = mgh + (1)/(2) mv^(2)`
`mg (R-Rcos theta) + (1)/(2) mxx (nh)/(2pim)sqrt((g)/(R))`
` (1)/(2) mgRxx x^(2)/R^(2)+ (1)/(2) (nh)/(4pi) sqrt((g)/(R))`
`(mg)/(2R)xx(nh)/(2pim)sqrt((R)/(g))+(nh)/(4pi)sqrt((g)/(R))`
` E = (nh)/(2pi) sqrt((g)/(R))`