Final value of a if distance between the points (-9 cm, a cm) and (3 cm, 3cm) is 13 cm.
To find the value of a such that the distance between the points (−9 cm,a cm) and (3 cm,3 cm) is 13 cm, we can use the distance formula.
1. Identify the Points:
Let the first point be P(−9,a) and the second point be Q(3,3).
2. Use the Distance Formula:
The distance d between two points (x1,y1) and (x2,y2) is given by:
d=√(x2−x1)2+(y2−y1)2
For our points, this becomes:
13=√(3−(−9))2+(3−a)2
3. Simplify the Expression:
Calculate 3−(−9):
3+9=12
So, we have:
13=√122+(3−a)2
4. Square Both Sides:
To eliminate the square root, square both sides:
132=122+(3−a)2
This simplifies to:
169=144+(3−a)2
5. Isolate the Squared Term:
Subtract 144 from both sides:
169−144=(3−a)2
Which gives:
25=(3−a)2
6. Take the Square Root:
Taking the square root of both sides:
√25=|3−a|
This results in two equations:
3−a=5or3−a=−5
7. Solve for a:
- From 3−a=5:
−a=5−3⟹−a=2⟹a=−2
- From 3−a=−5:
−a=−5−3⟹−a=−8⟹a=8
8. Final Values:
Thus, the possible values for a are:
a=−2ora=8
Summary:
The final values of a are −2 and 8.
Let the first point be P(−9,a) and the second point be Q(3,3).
The distance d between two points (x1,y1) and (x2,y2) is given by:
d=√(x2−x1)2+(y2−y1)2
For our points, this becomes:
13=√(3−(−9))2+(3−a)2
Calculate 3−(−9):
3+9=12
So, we have:
13=√122+(3−a)2
To eliminate the square root, square both sides:
132=122+(3−a)2
This simplifies to:
169=144+(3−a)2
Subtract 144 from both sides:
169−144=(3−a)2
Which gives:
25=(3−a)2
Taking the square root of both sides:
√25=|3−a|
This results in two equations:
3−a=5or3−a=−5
- From 3−a=5:
−a=5−3⟹−a=2⟹a=−2
- From 3−a=−5:
−a=−5−3⟹−a=−8⟹a=8
Thus, the possible values for a are:
a=−2ora=8
The final values of a are −2 and 8.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example
61 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Knowledge Check
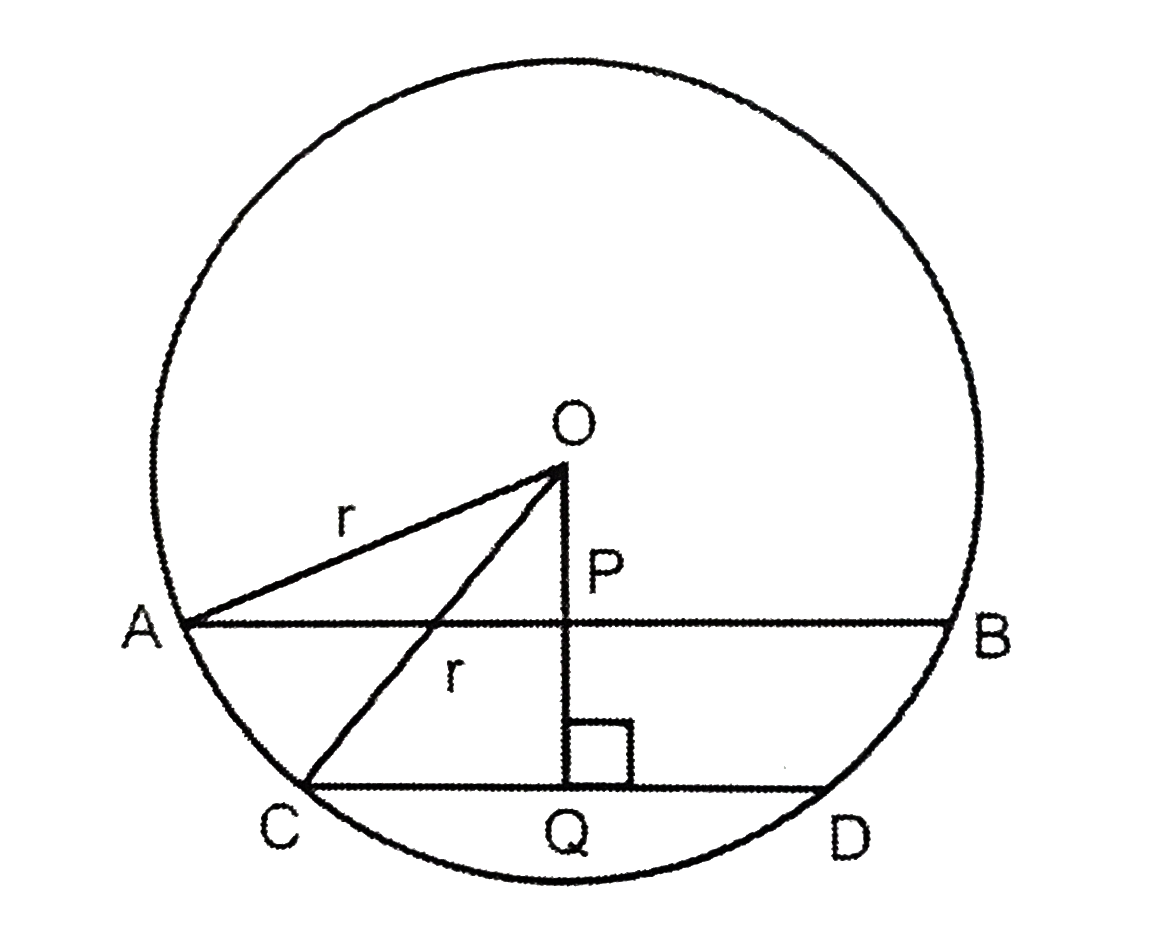
2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.A15 cmB14 cmC13 cmD12 cm
In the given diagram 'O is the centre of the circle and AB is parallel to CD. AB = 24 cm and distance between he chord AB and CD is 17 cm. It the radius of the circle is 13 cm, find the length of the chord CD.
View SolutionThe focal lengths of the objective and eyelens of a microscope are 1.6 cm and 2.5 cm respectively. The distance between the two lenses is 21.7 cm. If the final image is formed at infinity, the distance between the object and the objective lens is :
View SolutionThe focal lengths of the objective and eyelens of a microscope are 1.6 cm and 2.5 cm respectively. The distance between the two lenses is 21.7 cm. If the final image is formed at infinity, the distance between the object and the objective lens is :
View SolutionA compound microscope has an objective of focal length 2.0cm and an eye-piece of focal length 6.25cm and distance between the objective and eye-piece is 15cm. If the final image is formed at the least distance vision (25cm), the distance of the object form the objective is
View SolutionA parallelogram has sides of 15 cm and 12 cm. If the distance between the 15 cm sides is 6 cm, find the distance between 12 cm sides.
View SolutionA parallelogram has sides of 12 cm and 8 cm. If the distance between the 12 cm sides is 5 cm, find the distance between 8 cm sides.
View SolutionAn object is placed 20cm in front of a plane mirror. The mirror is moved 2cm towards the object. The distance between the positions of the original and final images seen in the mirror is (a) 2 cm (b) 4 cm (c) 10 cm (d) 22 cm
View Solution
