α and β are the angle made by a vector from positive x & positive y-axes redpectively. Which set of α and β is not possible
45∘,60∘
30∘,60∘
60∘,60∘
30∘,45∘
The correct Answer is:D
To solve the problem, we need to determine which set of angles α and β does not satisfy the condition for a vector in a two-dimensional plane. The condition we will use is:
cos2α+cos2β+cos2γ=1
where γ is the angle made with the z-axis. Since we are only concerned with α and β, we can rearrange this equation to find cos2γ:
cos2γ=1−cos2α−cos2β
The value of cos2γ must be between 0 and 1 (inclusive). Therefore, we need to check each set of angles provided in the options to see if they satisfy this condition.
1. Option 1: α=45∘,β=60∘
- Calculate cos2α and cos2β:
cos45∘=1√2⇒cos245∘=(1√2)2=12
cos60∘=12⇒cos260∘=(12)2=14
- Substitute into the equation:
cos2γ=1−(12+14)=1−34=14
- Since 14 is valid, this option is possible.
2. Option 2: α=30∘,β=60∘
- Calculate cos2α and cos2β:
cos30∘=√32⇒cos230∘=(√32)2=34
cos60∘=12⇒cos260∘=(12)2=14
- Substitute into the equation:
cos2γ=1−(34+14)=1−1=0
- Since 0 is valid, this option is possible.
3. Option 3: α=60∘,β=60∘
- Calculate cos2α and cos2β:
cos60∘=12⇒cos260∘=(12)2=14
cos60∘=12⇒cos260∘=(12)2=14
- Substitute into the equation:
cos2γ=1−(14+14)=1−12=12
- Since 12 is valid, this option is possible.
4. Option 4: α=30∘,β=45∘
- Calculate cos2α and cos2β:
cos30∘=√32⇒cos230∘=(√32)2=34
cos45∘=1√2⇒cos245∘=(1√2)2=12
- Substitute into the equation:
cos2γ=1−(34+12)=1−(34+24)=1−54=−14
- Since −14 is not valid (it is less than 0), this option is not possible.
Conclusion:
The set of angles α=30∘ and β=45∘ is not possible.
- Calculate cos2α and cos2β:
cos45∘=1√2⇒cos245∘=(1√2)2=12
cos60∘=12⇒cos260∘=(12)2=14
- Substitute into the equation:
cos2γ=1−(12+14)=1−34=14
- Since 14 is valid, this option is possible.
- Calculate cos2α and cos2β:
cos30∘=√32⇒cos230∘=(√32)2=34
cos60∘=12⇒cos260∘=(12)2=14
- Substitute into the equation:
cos2γ=1−(34+14)=1−1=0
- Since 0 is valid, this option is possible.
- Calculate cos2α and cos2β:
cos60∘=12⇒cos260∘=(12)2=14
cos60∘=12⇒cos260∘=(12)2=14
- Substitute into the equation:
cos2γ=1−(14+14)=1−12=12
- Since 12 is valid, this option is possible.
- Calculate cos2α and cos2β:
cos30∘=√32⇒cos230∘=(√32)2=34
cos45∘=1√2⇒cos245∘=(1√2)2=12
- Substitute into the equation:
cos2γ=1−(34+12)=1−(34+24)=1−54=−14
- Since −14 is not valid (it is less than 0), this option is not possible.
The set of angles α=30∘ and β=45∘ is not possible.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example61videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
α2,β2,γ2 are the angle which a line makes with positive x,y,z axes respectively. What is the value of cosα+cosβ+cosγ? (A) 1 (B) −1 (C) 2 (D) 3
View SolutionConsider the family of planes x+y+z=c where c is a parameter intersecting the coordinate axes P, Q andR and α,βandγ are the angles made by each member of this family with positive x, y and z-axes. Which of the following interpretations hold good got this family?
View SolutionIf α,βandγ are angles made by the line with positive direction of X-axis, Y-axis and Z-axis respectively, then find the value of cos2α+cos2β+cos2γ.
View SolutionIf α,β,γ be the angles which a line makes with the coordinates axes, then
View SolutionVector →P angle α,β and γ with the x,y and z axes respectively.
Then sin2α+sin2β+sin2γ=View SolutionThe vector →a=αˆi+2ˆj+βˆk lies in the plane of the vectors →b=ˆi+ˆj and →c=ˆj+ˆk and bisects the angle between →b and →c . Then which one of the following gives possible values of α and β ? (1) α=2,β=2 (2) α=1,β=2 (3) α=2,β=1 (4) α=1,β=1
View SolutionIf α,β,γ are the angles which a line makes with positive direction of the axes, then match the quantities in column-I to their values in column-II:
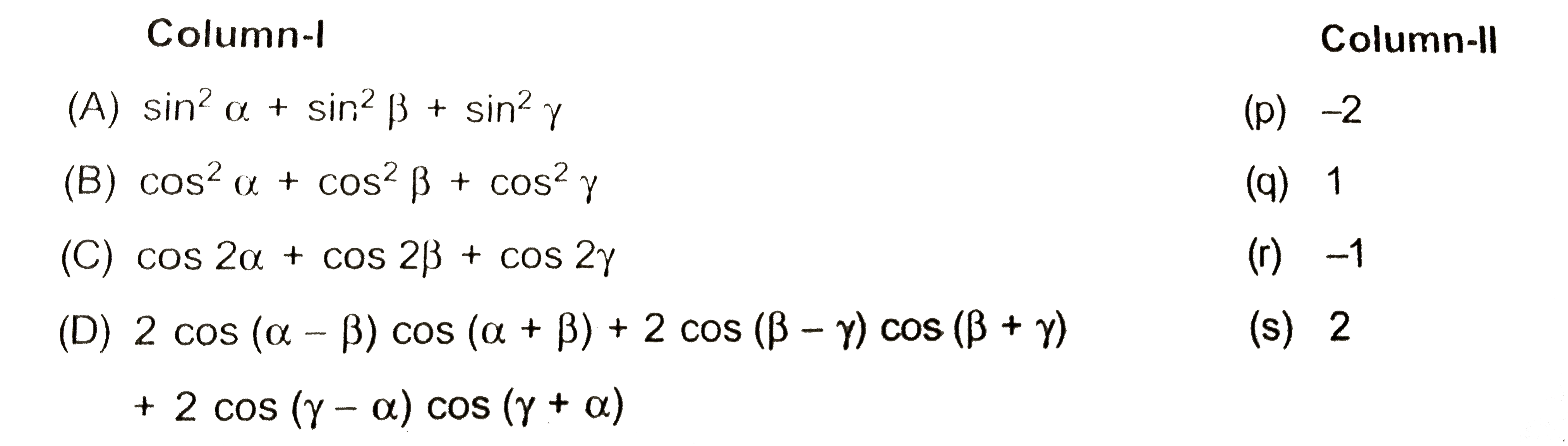 View Solution
View SolutionIf αandβ are acute angles and sinα=35,sinβ=817, find the values of sin(α+β),cos(α±β),andtan(α±β).
View Solutionαandβ are acute angles and cos2α=3cos2β−13−cos2β then tanαcotβ=
View SolutionThe vector →a=αˆi+2ˆj+βˆk lies in the plane of the vectors →b=ˆi+ˆj and →c=ˆj+ˆk and bisects the angle between →b and →c . Then which one of the following gives possible values of αandβ ? (1) α=2,β=2 (2) α=1,β=2 (3) α=2,β=1 (4) α=1,β=1
View Solution

