Forces proportional to AB,BC and 2CA act along the slides of a triangle ABC in magnitude and direction by
CA
AC
BC
CB
The correct Answer is:A
To solve the problem, we will analyze the forces acting along the sides of triangle ABC and apply the triangle law of vector addition.
1. Identify the Forces:
We have forces acting along the sides of triangle ABC. The forces are proportional to the lengths of the sides:
- Force along AB is proportional to AB
- Force along BC is proportional to BC
- Force along CA is proportional to 2CA
2. Express the Forces as Vectors:
We can denote the forces as vectors:
- Let →FAB be the force along AB.
- Let →FBC be the force along BC.
- Let →FCA be the force along CA.
According to the problem:
→FAB∝→AB,→FBC∝→BC,→FCA∝2→CA
3. Apply the Triangle Law of Vector Addition:
According to the triangle law of vector addition, the sum of the vectors around a closed triangle is zero:
→FAB+→FBC+→FCA=0
4. Rearranging the Equation:
From the equation above, we can rearrange it to express one of the forces in terms of the others:
→FAB+→FBC=−→FCA
5. Substituting the Given Proportions:
Given that →FCA is proportional to 2→CA, we can write:
→FAB+→FBC=−2→CA
6. Final Expression:
Rearranging gives us:
→FAB+→FBC+2→CA=0
7. Conclusion:
This indicates that the forces are balanced according to the triangle law of vector addition. The correct option based on our analysis is option A.
We have forces acting along the sides of triangle ABC. The forces are proportional to the lengths of the sides:
- Force along AB is proportional to AB
- Force along BC is proportional to BC
- Force along CA is proportional to 2CA
We can denote the forces as vectors:
- Let →FAB be the force along AB.
- Let →FBC be the force along BC.
- Let →FCA be the force along CA.
→FAB∝→AB,→FBC∝→BC,→FCA∝2→CA
According to the triangle law of vector addition, the sum of the vectors around a closed triangle is zero:
→FAB+→FBC+→FCA=0
From the equation above, we can rearrange it to express one of the forces in terms of the others:
→FAB+→FBC=−→FCA
Given that →FCA is proportional to 2→CA, we can write:
→FAB+→FBC=−2→CA
Rearranging gives us:
→FAB+→FBC+2→CA=0
This indicates that the forces are balanced according to the triangle law of vector addition. The correct option based on our analysis is option A.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-031videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-041videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)19videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
Three forces start acting simultaneously on a particle moving with velocity, →v. These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity
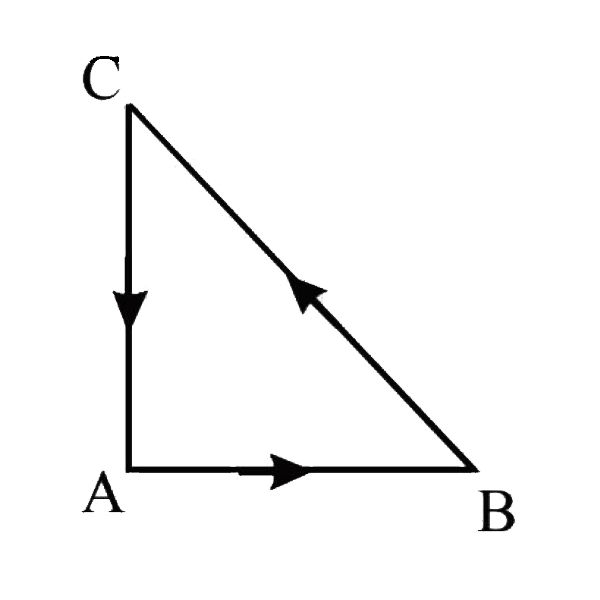 View Solution
View SolutionThe cube as shown in Fig. 1.61, 75.0 cm on a side, is placed in a uniform magnetic field of 0.860 T parallel to the x-axis. The wire abcdef carries a current of 6.58 A in the direction indicated.
(a) Determine the magnitude and direction of the force acting on the segment ab.
(b) Determine the magnitude and direction of the force acting on the sement bc.
(c) Determine the magnitude and direction of the force acting on the segment cd.
(d) Determine the magnitude and direction of the force acting on the segment de.
(e) Determine the magnitude and direction of the force acting on the segment ef.
(f) What are the magnitude and direction of the total force on the wire ?
 View Solution
View SolutionThree forces start acting simultaneously on a particle moving with velocity →v. These forces are represented in magnitude and direction by the three sides os a triangle ABC (as shown). The particle will now move with velocity.
 View Solution
View SolutionA current carrying closed loop in the from of a right angle isoseles triangle ABC is placed in a unifrom magnetic fild acting along AB. If the magnetic force on the arm BC is F, the force on the arm AC is
 View Solution
View SolutionIf D(-2, 3), E (4, -3) and F (4, 5) are the mid-points of the sides BC, CA and AB of the sides BC, CA and AB of triangle ABC, then find √(|AG|2+|BG|2−|CG|2) where, G is the centroid of ΔABC.
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that ΔDEF is also isosceles.
View SolutionABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is
 View Solution
View SolutionAM is a median of s triangle ABC. Is AB+BC+CA>2AM? (Consider the sides of triangles ΔABMandΔAMC.
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionABC is an isosceles triangle right angled at A. forces of magnitude 2√2,5and6 act along BC, CA and AB respectively. The magnitude of their resultant force is
View Solution

