Column IColumn II(A)Dimensional variable(p)π(B)Dimensionless variable(q)Force(C)Dimensional constant(r)Angle(D)Dimensionless constant(s)Gravitational constant
The correct Answer is:(A)-q, (B)-r, (C)-s, (D)-p
To solve the problem of matching the items in Column I with those in Column II, we will analyze each item based on its dimensional properties.
1. Identify the nature of each item in Column I:
- A: Dimensional variable
- B: Dimensionless variable
- C: Dimensional constant
- D: Dimensionless constant
2. Analyze the items in Column II:
- p: π (pi)
- q: Force
- r: Angle
- s: Gravitational constant
3. Match each item:
- For p (π):
- The dimensional formula for π is m0l0t0, which means it has no dimensions. Therefore, π is a dimensionless constant.
- Match: D (Dimensionless constant) with p (π).
- For q (Force):
- The dimensional formula for force is m1l1t−2. This shows that force has dimensions.
- Match: A (Dimensional variable) with q (Force).
- For r (Angle):
- The dimensional formula for angle is also m0l0t0, indicating that angle is dimensionless.
- Match: B (Dimensionless variable) with r (Angle).
- For s (Gravitational constant):
- The dimensional formula for the gravitational constant is m1l3t−2. This indicates that it has dimensions and is a constant.
- Match: C (Dimensional constant) with s (Gravitational constant).
4. Final Matches:
- A → q (Force)
- B → r (Angle)
- C → s (Gravitational constant)
- D → p (π)
Summary of Matches:
- A (Dimensional variable) → q (Force)
- B (Dimensionless variable) → r (Angle)
- C (Dimensional constant) → s (Gravitational constant)
- D (Dimensionless constant) → p (π)
- A: Dimensional variable
- B: Dimensionless variable
- C: Dimensional constant
- D: Dimensionless constant
- p: π (pi)
- q: Force
- r: Angle
- s: Gravitational constant
- For p (π):
- The dimensional formula for π is m0l0t0, which means it has no dimensions. Therefore, π is a dimensionless constant.
- Match: D (Dimensionless constant) with p (π).
- The dimensional formula for force is m1l1t−2. This shows that force has dimensions.
- Match: A (Dimensional variable) with q (Force).
- The dimensional formula for angle is also m0l0t0, indicating that angle is dimensionless.
- Match: B (Dimensionless variable) with r (Angle).
- The dimensional formula for the gravitational constant is m1l3t−2. This indicates that it has dimensions and is a constant.
- Match: C (Dimensional constant) with s (Gravitational constant).
- A → q (Force)
- B → r (Angle)
- C → s (Gravitational constant)
- D → p (π)
- A (Dimensional variable) → q (Force)
- B (Dimensionless variable) → r (Angle)
- C (Dimensional constant) → s (Gravitational constant)
- D (Dimensionless constant) → p (π)
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - ASSERTION-REASON
18 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 1
5 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-01
87 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Match the extraction processes listed in Column I with metals listed in Column II.
Column IColumn II(A)Self reduction(p)Lead(B)Carbon reduction(q)Silver(C)Complex formation and displacement by metal(r)Copper(D)Decomposition of iodide(s)Boron
View SolutionColumn IColumn II(A)Stress(p)Pressure(B)Strain(q)Energy density(C)Modulus of elasticity(r)Angle(D)Torque(s)Energy
View Solutiong is dimensional constant where as π is the dimensionless constant. Why?
View SolutionMatch the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinity
View SolutionMatch Column I with Column II and select the correct option .
Column IColumn II(A)AIDS(p)Yersinia pestis(B)Syphilis (q)Hepatitis virus(C)Viral jaundice(r)HIV(D)Gonorrhea(s)Treponema(t)Neisseria
View SolutionColumn-IColumn-II(a)Crypts of Liberkuhn (p)Loop of duodenum(b)Pancreas(q)Stomach(c)Adrenal gland(r)Intestine(d)Gastric glands (s)Kidney
View SolutionTwo concentric spherical shells are as shown in figure. Match the following columns
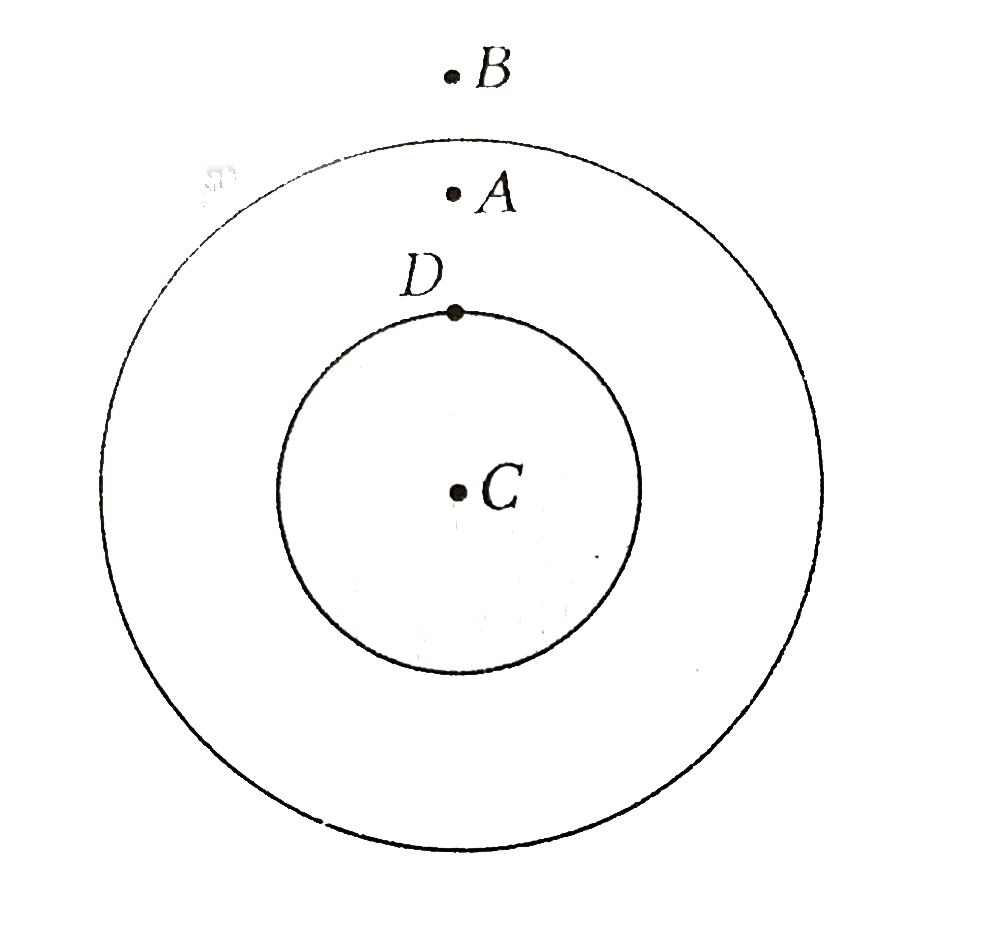
Column-IColumn-II(A)Potential at A(p)greater than B(B)Gravitational field at A(q)less than B(C)As one moves from C to D(r)Potential remains constant(D)As one moves from D to A(s)Gravitational field decreases(t)None
View SolutionIn y=Asinωt+Asin(ωt+2π3)
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Column-IColumn-II(A)Motion(p)is periodic but no SHM(B)Amplitude(q)is SHM(C)Initial phase(r)A(D)Maximum velocity(s)π/3(t)ωA/2(u)None∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionIf net force on a system of particles is zero. Then
Column IColumn II(A)Acceleration of centre of mass(p)Constant(B)Velocity of centre of mass(q)Zero(C)Momentum of centre of mass(r)May be zero(D)Velocity of an individual particle of the system(s)May be constant
View SolutionColumn IColumn II(A)R/L(p)Time(B)C/R(q)Frequency(C)E/B(r)Speed(D)√ε0μ0(s)None
View Solution
