A proton sists at coordinates (x,y)=(0, 0), and an electron at (d, h), where d>>h. At time t=0 a uniform electric field E of unknown magnitude but pointing in the positive y direction is turned on. Assuming that d is large enough that the proton electron interaction is negligible, the y coordinates of the two particles will be equal (at equal time)
at about y =h/2000
at an undetermined value since E is unknown,
at about y=h/43,
nowhere: they move in opposite sirections
The correct Answer is:A
To solve the problem, we need to analyze the motion of a proton and an electron in a uniform electric field directed in the positive y-direction. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Conditions
- The proton is at coordinates (0, 0) and the electron is at (d, h) where d≫h.
- An electric field E is turned on at t=0 in the positive y-direction.
Hint: Identify the initial positions of the particles and the direction of the electric field.
Step 2: Determine the Forces Acting on Each Particle
- The force on the proton (Fp) due to the electric field is given by:
Fp=qpE
where qp is the charge of the proton.
- The force on the electron (Fe) is:
Fe=qeE
where qe is the charge of the electron (note that qe is negative).
Hint: Recall that the force on a charged particle in an electric field is given by F=qE.
Step 3: Calculate the Accelerations of Each Particle
- The acceleration of the proton (ap) is:
ap=Fpmp=qpEmp
- The acceleration of the electron (ae) is:
ae=Feme=qeEme
Hint: Use Newton's second law F=ma to express the accelerations in terms of the forces and masses.
Step 4: Write the Equations of Motion
- For the proton, starting from rest, the distance traveled in the y-direction (y) after time t is:
y=12apt2=12(qpEmp)t2
- For the electron, the distance traveled in the y-direction (h) is:
h′=12aet2=12(−qeEme)t2
Hint: Remember that the electron moves in the opposite direction due to its negative charge.
Step 5: Set the Distances Equal
At equal time t, we want to find when the y-coordinates of the proton and electron are equal:
y=h′
Substituting the expressions from Step 4:
12(qpEmp)t2=12(−qeEme)t2
Hint: Cancel out common factors and simplify the equation.
Step 6: Solve for the Ratio of Distances
Cancelling t2 and 12 from both sides gives:
qpmp=−qeme
From this, we can express the ratio of the distances traveled by the proton and electron:
yh=memp
Hint: Use the known mass ratio of the proton and electron to simplify further.
Step 7: Substitute Known Mass Values
The mass of the proton mp is approximately 1836 times the mass of the electron me:
yh=me1836me=11836
Thus, we find:
y=h1836
Hint: Ensure you understand how the mass ratio affects the final distance traveled.
Conclusion
The y-coordinate of the proton will be equal to h1836 when the y-coordinate of the electron is h.
Final Answer
The y-coordinate of the proton when it equals the y-coordinate of the electron is:
y=h1836
- The proton is at coordinates (0, 0) and the electron is at (d, h) where d≫h.
- An electric field E is turned on at t=0 in the positive y-direction.
- The force on the proton (Fp) due to the electric field is given by:
Fp=qpE
where qp is the charge of the proton.
- The force on the electron (Fe) is:
Fe=qeE
where qe is the charge of the electron (note that qe is negative).
- The acceleration of the proton (ap) is:
ap=Fpmp=qpEmp
- The acceleration of the electron (ae) is:
ae=Feme=qeEme
- For the proton, starting from rest, the distance traveled in the y-direction (y) after time t is:
y=12apt2=12(qpEmp)t2
- For the electron, the distance traveled in the y-direction (h) is:
h′=12aet2=12(−qeEme)t2
At equal time t, we want to find when the y-coordinates of the proton and electron are equal:
y=h′
Substituting the expressions from Step 4:
12(qpEmp)t2=12(−qeEme)t2
Cancelling t2 and 12 from both sides gives:
qpmp=−qeme
From this, we can express the ratio of the distances traveled by the proton and electron:
yh=memp
The mass of the proton mp is approximately 1836 times the mass of the electron me:
yh=me1836me=11836
Thus, we find:
y=h1836
The y-coordinate of the proton will be equal to h1836 when the y-coordinate of the electron is h.
The y-coordinate of the proton when it equals the y-coordinate of the electron is:
y=h1836
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-037videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - ASSERTION-REASON18videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
There exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionA uniform electric field exists in x y plane as shown in Fig. 3.45. Find the potential difference. Between origin O and A(d,d,0).
 .View Solution
.View SolutionAn electron is moving along +x direction with a velocity of 6×106ms−1 . It enters a region of uniform electric field of 300 V/cm pointing along + y direction. The magnitude and direction of the magnetic field set up in this region such that the electron keeps moving along the x direction will be :
View SolutionUniform electric field E and magnetic field B, respectively, are along y-axis as shown in the figure. A particle with specific charge q/m leaves the origin O in the direction of x-axis with an initial non-relativistic speed v0.Thec∞rd∈ateY_(n) of the particle when it crosses the y-axis for the nth time is:
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on isView SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic field of strength B is also switched on along positive y-axis.
Velocity of the particle just before the magnetic field is switched on isView SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
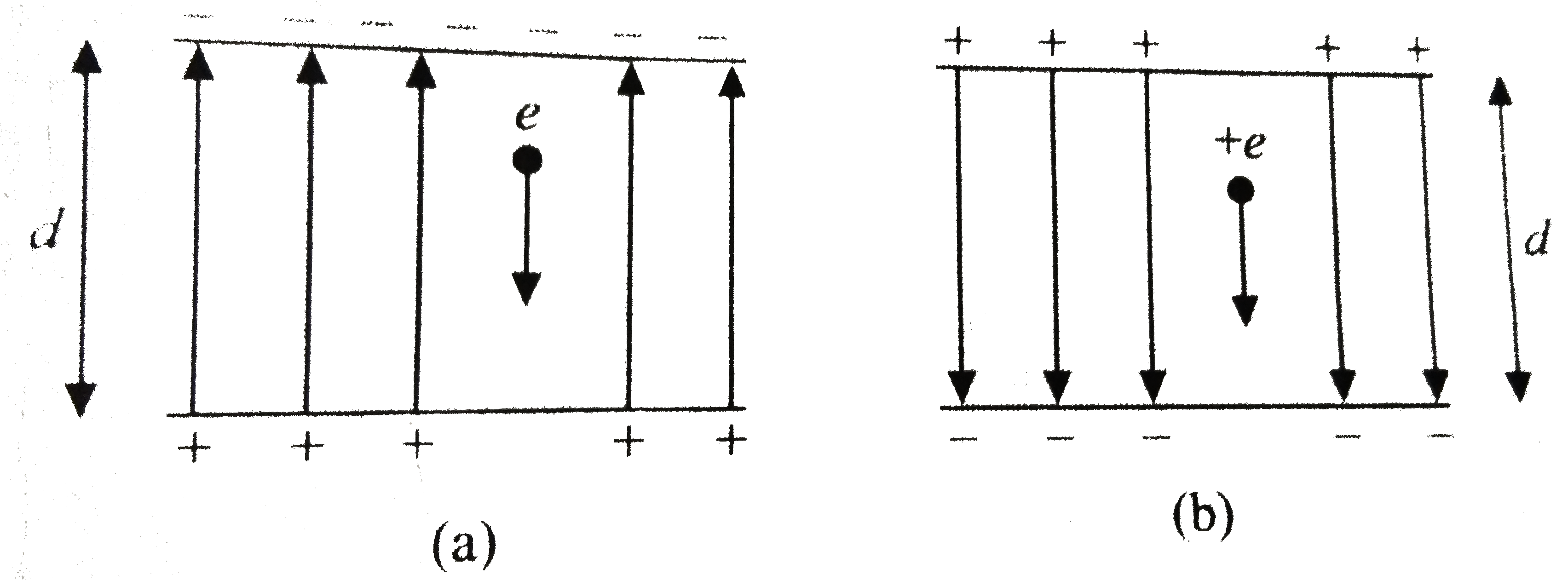 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.View SolutionAn electron moving with a speed u along the positive x-axis at y=0 enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then
 View Solution
View SolutionAn electron moving with a speed u along the positive x-axis at y=0 enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then
 View Solution
View Solution

