A sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:
Q∈0
Q2∈0
4Q∈0
2Q∈0
The correct Answer is:A
To solve the problem of finding the electric flux through an imaginary sphere of radius 2R that encloses a sphere of radius R with charge Q, we can use Gauss's Law. Here’s the step-by-step solution:
Step 1: Understand Gauss's Law
Gauss's Law states that the electric flux (Φ) through a closed surface is equal to the charge (Q_enc) enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it is expressed as:
\(
\Phi = \frac{Q_{\text{enc}}}{\epsilon_0}
\)
Step 2: Identify the Charge Enclosed
In this scenario, we have a sphere of radius R with charge Q placed inside an imaginary sphere of radius 2R. Since the charge Q is fully enclosed by the imaginary sphere, we can say that:
\(
Q_{\text{enc}} = Q
\)
Step 3: Apply Gauss's Law
Now, we can apply Gauss's Law to find the electric flux through the imaginary sphere of radius 2R:
\(
\Phi = \frac{Q}{\epsilon_0}
\)
Step 4: Conclusion
Thus, the electric flux related to the imaginary sphere is:
\(
\Phi = \frac{Q}{\epsilon_0}
\)
Now, we can check the options provided in the question to find the correct answer.
Final Answer
The flux related to the imaginary sphere is:
\(
\Phi = \frac{Q}{\epsilon_0}
\)
Gauss's Law states that the electric flux (Φ) through a closed surface is equal to the charge (Q_enc) enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it is expressed as:
\Phi = \frac{Q_{\text{enc}}}{\epsilon_0}
\)
In this scenario, we have a sphere of radius R with charge Q placed inside an imaginary sphere of radius 2R. Since the charge Q is fully enclosed by the imaginary sphere, we can say that:
Q_{\text{enc}} = Q
\)
Now, we can apply Gauss's Law to find the electric flux through the imaginary sphere of radius 2R:
\Phi = \frac{Q}{\epsilon_0}
\)
Thus, the electric flux related to the imaginary sphere is:
\Phi = \frac{Q}{\epsilon_0}
\)
The flux related to the imaginary sphere is:
\Phi = \frac{Q}{\epsilon_0}
\)
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-03
7 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - ASSERTION-REASON
18 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
A conducting sphere of radius r has a charge . Then .
View SolutionA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Now the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would be
View SolutionA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Then the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would becomes V/n. find value of n
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
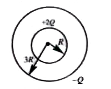
What would be the final distribution of charges if the sphres are joined by a conducting wire
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
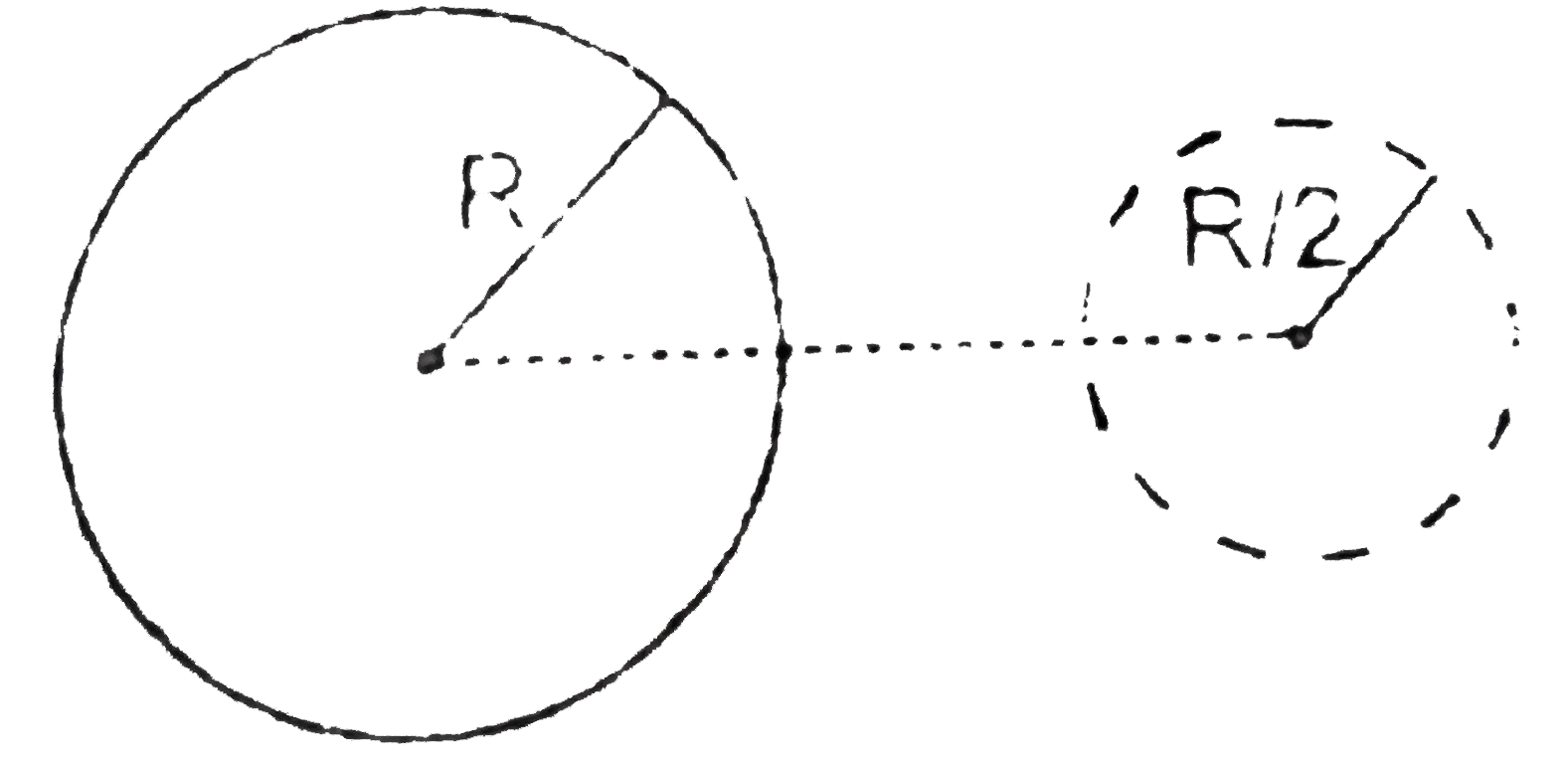
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R

View SolutionA large insulated sphere of radius r charged with Q units of electricity is placed in contact with a small insulated uncharged sphere of radius r' and is then separated. The charge on the smaller sphere will now be.
View Solution
consider a neutral conducting sphere of radius a with a spherical cavity of radius b. A charged conducting sphere of radius c is placed in cavity . Centre of this sphere coincide with centre of cavity charge on the inner sphere is q total self energy of this arrangement is:
View Solution
