Question

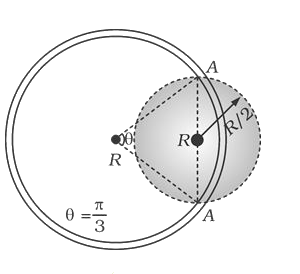
A ring of radius $R$ having a linear charge density $\lambda$ moves towards a solid imaginary sphere of radius $\frac{R}{2}$, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is

Answer

D

Explanation

Electric flux will be maximum when maximum length of ring is inside the sphere. This will occur when the length of the chord AB is maximum. Now maximum length of chord AB can be the diameter of the ring. In this case of the arc of ring inside the sphere subtends an angle of at the centre of ring. Thus charge on this arc in this situation is given as
`q=(R pi)/3. lamda implies phi =(R pi)/(3/e_0) lamda= (R pi lamda)/(3 e_0)`