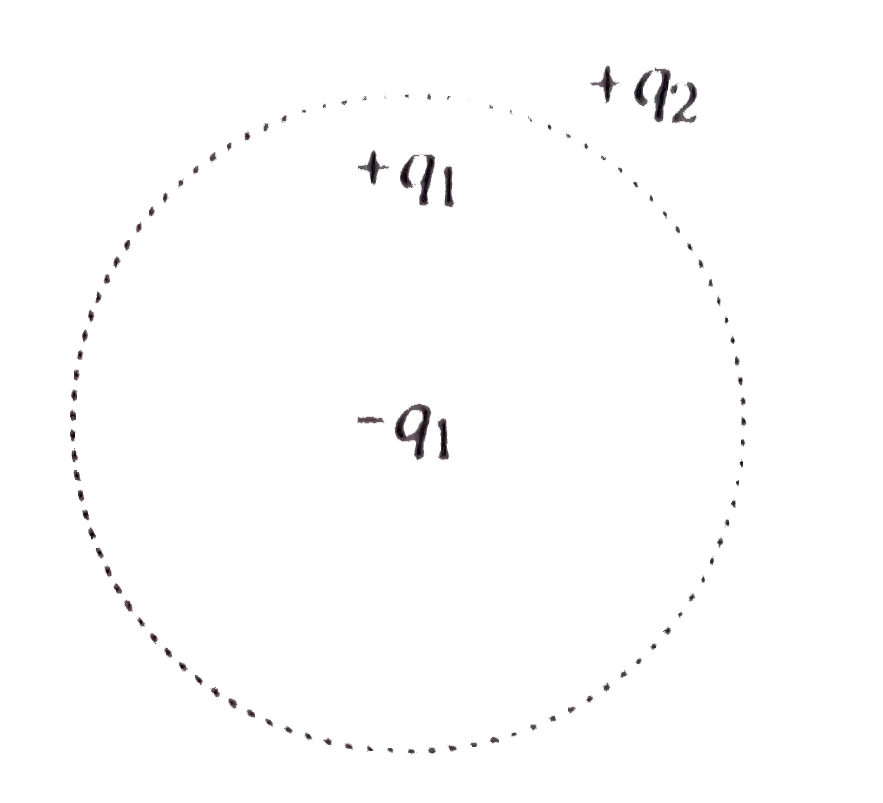
Consider the charge configuration and spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface the electric field will be due to
q2
only the positive charges
all the charges
+q1 and −q1
The correct Answer is:C
At any point over the spherical Gaussian surface, net electric field is the vector sum of electric field due to +q1,−q1 and q2.
Don't confuse with the electric flux which is zero (net) passing over the Gaussian surface as the net charge enclosing the surface is zero.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - MCQ s WITH ONE OR MORE THAN ONE CORRECT ANSWER6videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - REASONING TYPE1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(A)35videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
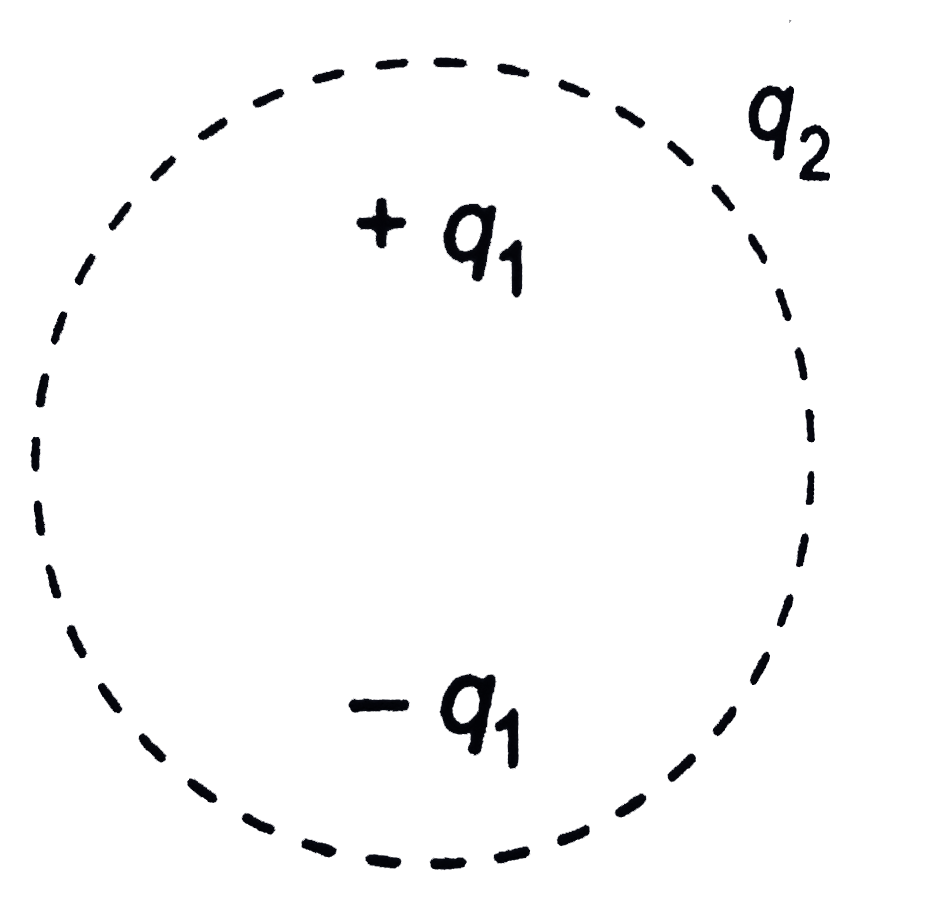
Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
 View Solution
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
 View Solution
View SolutionIf the flux of the electric field through a closed surface is zero,
View SolutionElectric flux through a spherical surface shown in the figure is
 _______View Solution
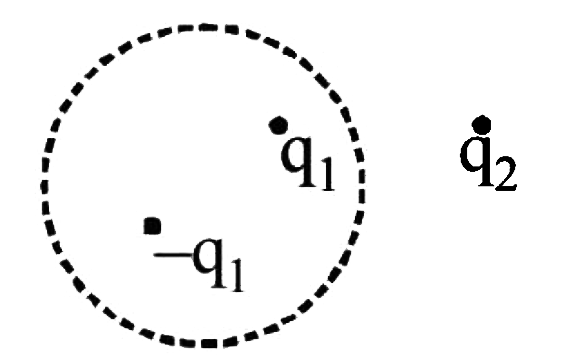
_______View SolutionA Gausisan surface in the figure is shown by dotted line.
The electric field on the surface will be
 View Solution
View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
View SolutionFind the flux due to the electric field through the curved surface (R is radius of curvature)
 View Solution
View SolutionThe Gaussian surface for calculating the electric field due to a charge distribution is
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionA small metal sphere carrying charge +Q is located at the centre of a spherical cavity inside a large uncharged metallic spherical shell as shown in the figure. Use Gauss’s law to find the expressions for the electric field at points p1 and p2 . Also draw the pattern of electric field lines in this arrangement.
 View Solution
View Solution

