A positively charged thin metla ring of radius R is fixed in the X-Y plane with its centre is the origin O. A negatively charged particle P is released from rest at the point (0,0,Z0) where (Z0>0). Then the motion of P is
pariodic for all values of z0 satisfying 0<z0<∞
simple harmonic for all values of z0 satisfying 0<z0≤R
approximately simple harmonic provided z0<<R
such that P crosses O and continues to move along negative z-axis towards z=−∞
The correct Answer is:A, C
Let Q be the charge on the ring, the negative charge -q is released from point P(0,0,z0). The electric field at P due to the charged ring will be along positive z-axis and its magnitude will be
E=14πε0Qz0(R2+z20)3/2
E=0 at centre of the ring because z0=0
Therefore, force on charge P will be towards centre as shown, and its magnitude is
Fe=qE=14πε0Qq(R2+z20)3/2.z0 ...(i)
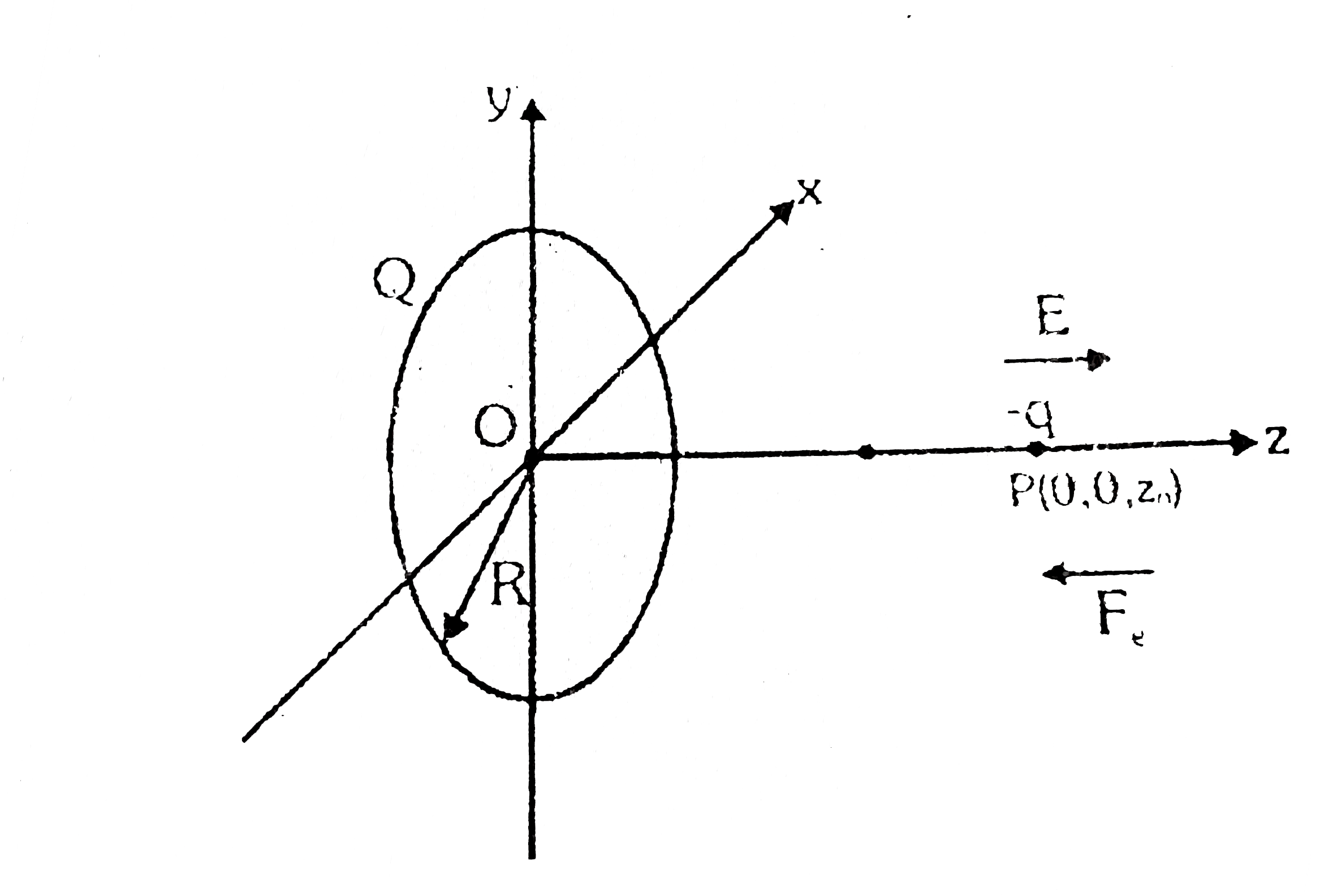
Similarly, when it courses the origin, the force is again towards centre O.
Thus, the motion of the particle is periodic for all values of z0 lying between 0 and ∞.
Secondly, if z0<<R,(R2+z20)3/2≈R3
z0<<R,(R2+z20)3/2≈R3
Fe≈−14πε0.QqR3.z0 (From Eq. 1)
i.e., the restoring force Fe∝−z0. Hence, the motion of the particle will be simple harmonic. (Here negative sign implies that the force is towards its mean position).
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - REASONING TYPE1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - MATCH THE COLUME TYPE1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)19videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
A positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
View SolutionA positively charged ring is in y - z plane with its centre at origin . A positive test charge qe , held at origin is released along x axis, then its speed
View Solution
Knowledge Check
- Question 1 - Select One
A positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
Aperiodic for all values of Z0 satisfying 0<Z0<∞Bsimple harmonic for all values of Z0 satisfying 0<Z0≤RCapproximately simple harmonic provided Z0<<RDsuch that P crosses O and continues to move along the negative Z-axis towards Z=−∞
A circular ring of radius R with uniform positive charge density λ per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point p(−√3R,0,0) on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View SolutionA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
View SolutionA charge q=10μC is distributed uniformly over the circumference of a ring of radius 3m placed on x-y placed with its centre art origin. Find the electric potential at a point P(0,0,4m)
View SolutionA charge q=10μC is distributed uniformly over the circumference of a ring of radius 3m placed on x-y placed with its centre art origin. Find the electric potential at a point P(0,0,4m)
View SolutionTwo equal negative charges −q are fixed at points (0,−a) and (0,a) on y-axis. A poistive charge Q is released from rest at point (2a,0) on the x-axis. The charge Q will
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
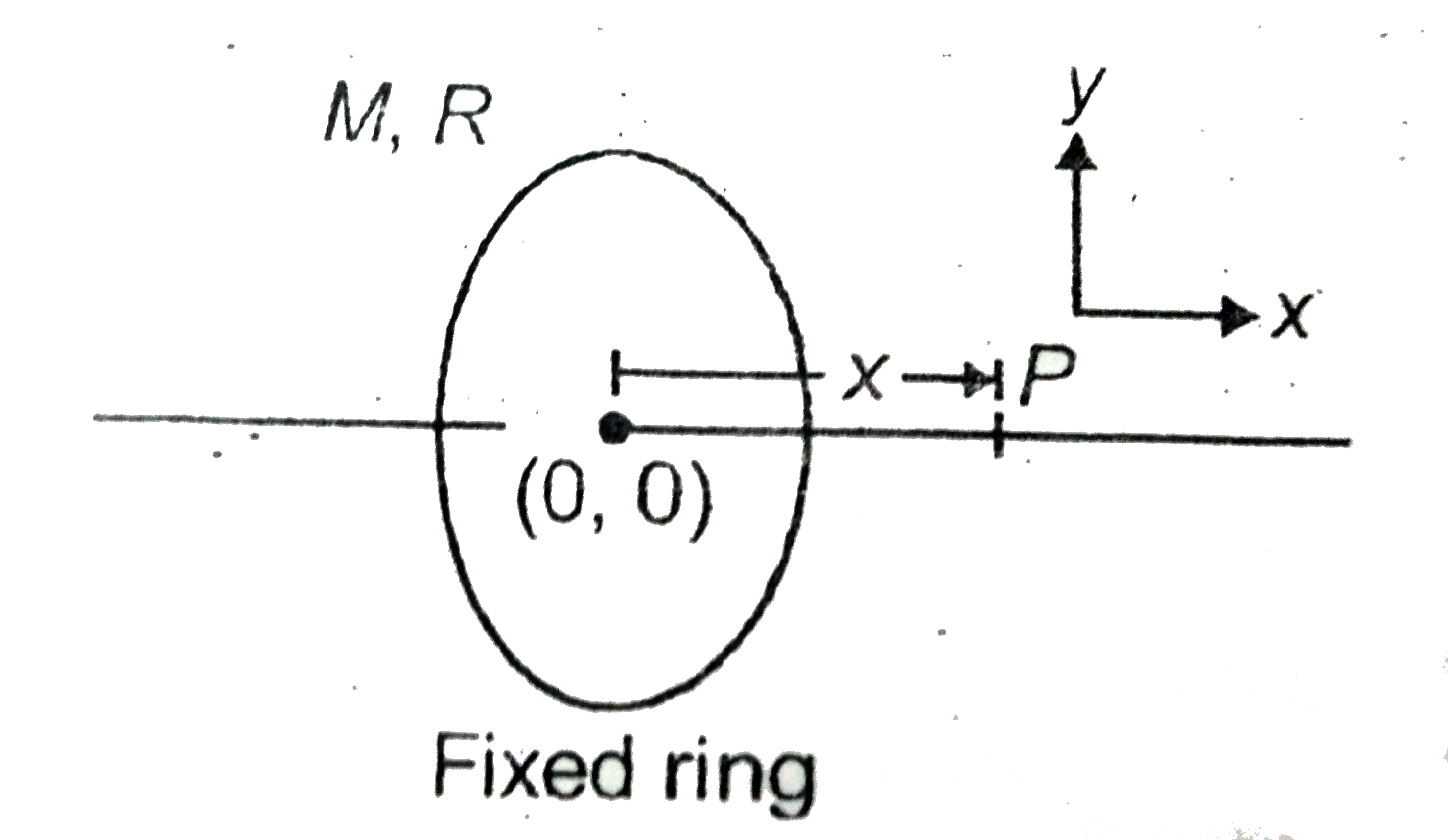
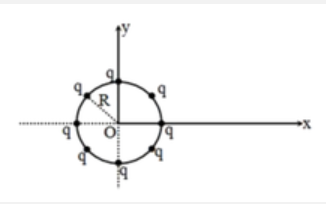
If the particle (mass m) is released from rest from a point distant x=R√3, then it will pass through the centre of ring with speedView SolutionEight charges each of value q are placed on a ring of radius R placed in x - y plane with origin at centre . A - q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v . The velocity of - q when it reaches the centre of ring is (neglect gravity)
 View Solution
View Solution

