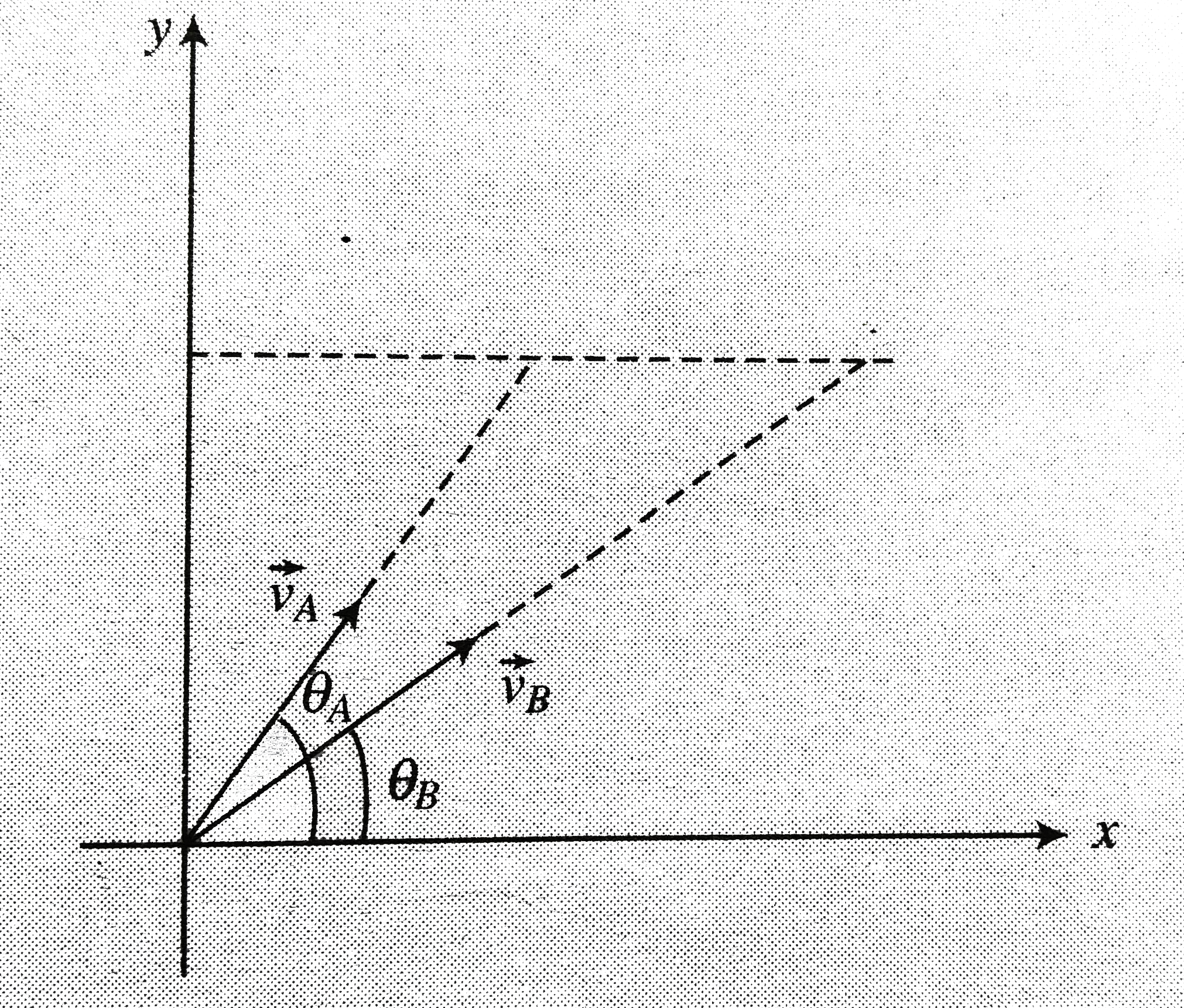
Two particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
 .
.
TA=TB
TA>TB
TA<TB
Can't be determined
The correct Answer is:A
y−component of velocity is same for both the particles. TA=TB
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - Exercise (Physics)
330 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Two particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
 .
.
View SolutionTwo particles of charges +Q and −Q are projected from the same point with a velocity v in a region of unifrom magnetic filed B such that the velocity vector makes an angle 'theta' with the magnetic filed Their masses are M and 2M respectively Then, they will meet again for the first time at a point whose distane from the point of projection is .
View SolutionTwo particle A and B projected along different directions from the same point P on the ground with the same velocity of 70 m/s in the same vertical plane. They hit the ground at the same point Q such that PQ = 480,. Then [g=9.8m/s2]
View SolutionThere are two angles of projection for which the horizontal range is the same. Show that the sum of the maximum heights for these two angles is independent of the angle of projection.
View SolutionTwo particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
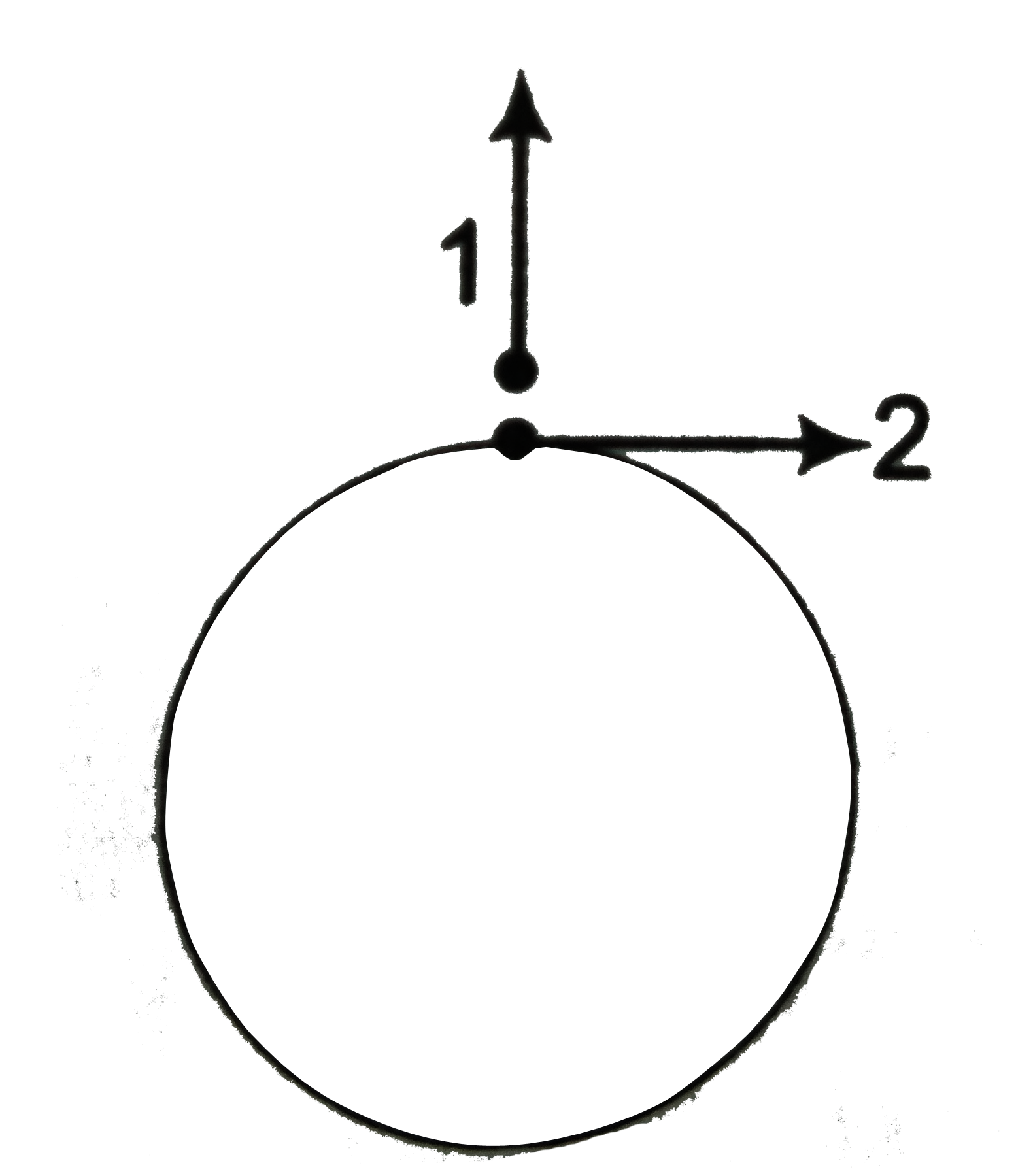
View SolutionTwo identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
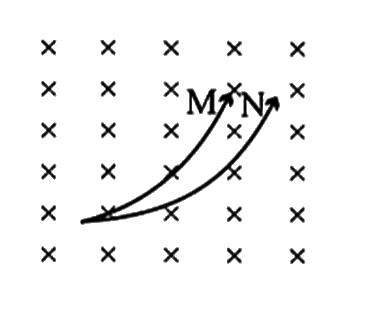
View SolutionTwo charged particle M and N are projected with same velocity in a uniform magnetic field. Then M and N respectively.
View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 & θ2 to the horizontal. They have the same range. Their times of flight are t1 & t2 respectily
View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 & θ2 to the horizontal. They have the same range. Their times of flight are t1 & t2 respectfully
View SolutionTwo particles are projected from the same point making angles angle θ1 and θ2 with the horizontal respectively in such a way that their horizontal velocities are equal. The ratio of maximum heights (H1H2) will be equal to
View Solution
