Two particle A and B projected along different directions from the same point P on the ground with the same velocity of 70 m/s in the same vertical plane. They hit the ground at the same point Q such that PQ = 480,. Then [g=9.8m/s2]
Ratio of their times of flight is 4:5
Ratio of their maximum heights is 9:16
Ratio of their minimum speeds during flights is 4:3
The bisector of the angle between their directions of projection makes 45∘ with horizontal
The correct Answer is:B, C, D
To solve the problem step by step, we will analyze the projectile motion of two particles A and B, which are projected from the same point P with the same initial velocity and hit the ground at the same point Q.
Step 1: Understanding the Problem
We have two particles A and B projected at the same initial velocity u=70m/s at angles θA and θB respectively. They hit the ground at the same horizontal distance PQ=480m. The acceleration due to gravity g=9.8m/s2.
Step 2: Range of Projectile Motion
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
Since both particles hit the same point Q, their ranges are equal:
RA=RB=480m
Thus, we can write:
480=702sin(2θA)9.8
480=702sin(2θB)9.8
Step 3: Solving for Angles
From the range formula for particle A:
480=4900sin(2θA)9.8
Rearranging gives:
sin(2θA)=480×9.84900
Calculating this:
sin(2θA)=47044900≈0.96
Now, we can find 2θA:
2θA=sin−1(0.96)≈73.74∘
Thus,
θA≈36.87∘
Since θA+θB=90∘:
θB=90∘−θA≈53.13∘
Step 4: Time of Flight
The time of flight T for projectile motion is given by:
T=2usin(θ)g
Thus, for particles A and B:
TA=2×70sin(36.87∘)9.8
TB=2×70sin(53.13∘)9.8
Calculating the sine values:
sin(36.87∘)≈0.6andsin(53.13∘)≈0.8
Thus:
TA≈2×70×0.69.8≈8.57s
TB≈2×70×0.89.8≈10.14s
Step 5: Maximum Height
The maximum height H is given by:
H=u2sin2(θ)2g
Calculating for both particles:
HA=702sin2(36.87∘)2×9.8
HB=702sin2(53.13∘)2×9.8
Calculating:
HA≈4900×0.3619.6≈90.0m
HB≈4900×0.6419.6≈160.0m
Step 6: Minimum Speed During Flight
The minimum speed occurs at the maximum height, which is given by the horizontal component of the velocity:
Vmin=ucos(θ)
Calculating for both particles:
VminA=70cos(36.87∘)≈70×0.8=56m/s
VminB=70cos(53.13∘)≈70×0.6=42m/s
Step 7: Conclusion
Based on the calculations:
- The angles of projection are approximately 36.87∘ and 53.13∘.
- The ratio of time of flight TA:TB is approximately 3:4.
- The ratio of maximum heights HA:HB is 9:16.
- The ratio of minimum speeds VminA:VminB is 4:3.
We have two particles A and B projected at the same initial velocity u=70m/s at angles θA and θB respectively. They hit the ground at the same horizontal distance PQ=480m. The acceleration due to gravity g=9.8m/s2.
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
Since both particles hit the same point Q, their ranges are equal:
RA=RB=480m
Thus, we can write:
480=702sin(2θA)9.8
480=702sin(2θB)9.8
From the range formula for particle A:
480=4900sin(2θA)9.8
Rearranging gives:
sin(2θA)=480×9.84900
Calculating this:
sin(2θA)=47044900≈0.96
2θA=sin−1(0.96)≈73.74∘
Thus,
θA≈36.87∘
θB=90∘−θA≈53.13∘
The time of flight T for projectile motion is given by:
T=2usin(θ)g
Thus, for particles A and B:
TA=2×70sin(36.87∘)9.8
TB=2×70sin(53.13∘)9.8
sin(36.87∘)≈0.6andsin(53.13∘)≈0.8
Thus:
TA≈2×70×0.69.8≈8.57s
TB≈2×70×0.89.8≈10.14s
The maximum height H is given by:
H=u2sin2(θ)2g
Calculating for both particles:
HA=702sin2(36.87∘)2×9.8
HB=702sin2(53.13∘)2×9.8
HA≈4900×0.3619.6≈90.0m
HB≈4900×0.6419.6≈160.0m
The minimum speed occurs at the maximum height, which is given by the horizontal component of the velocity:
Vmin=ucos(θ)
Calculating for both particles:
VminA=70cos(36.87∘)≈70×0.8=56m/s
VminB=70cos(53.13∘)≈70×0.6=42m/s
Based on the calculations:
- The angles of projection are approximately 36.87∘ and 53.13∘.
- The ratio of time of flight TA:TB is approximately 3:4.
- The ratio of maximum heights HA:HB is 9:16.
- The ratio of minimum speeds VminA:VminB is 4:3.
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
Two particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
 .
.
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View Solution
Knowledge Check
A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 s
Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:

View SolutionTwo particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
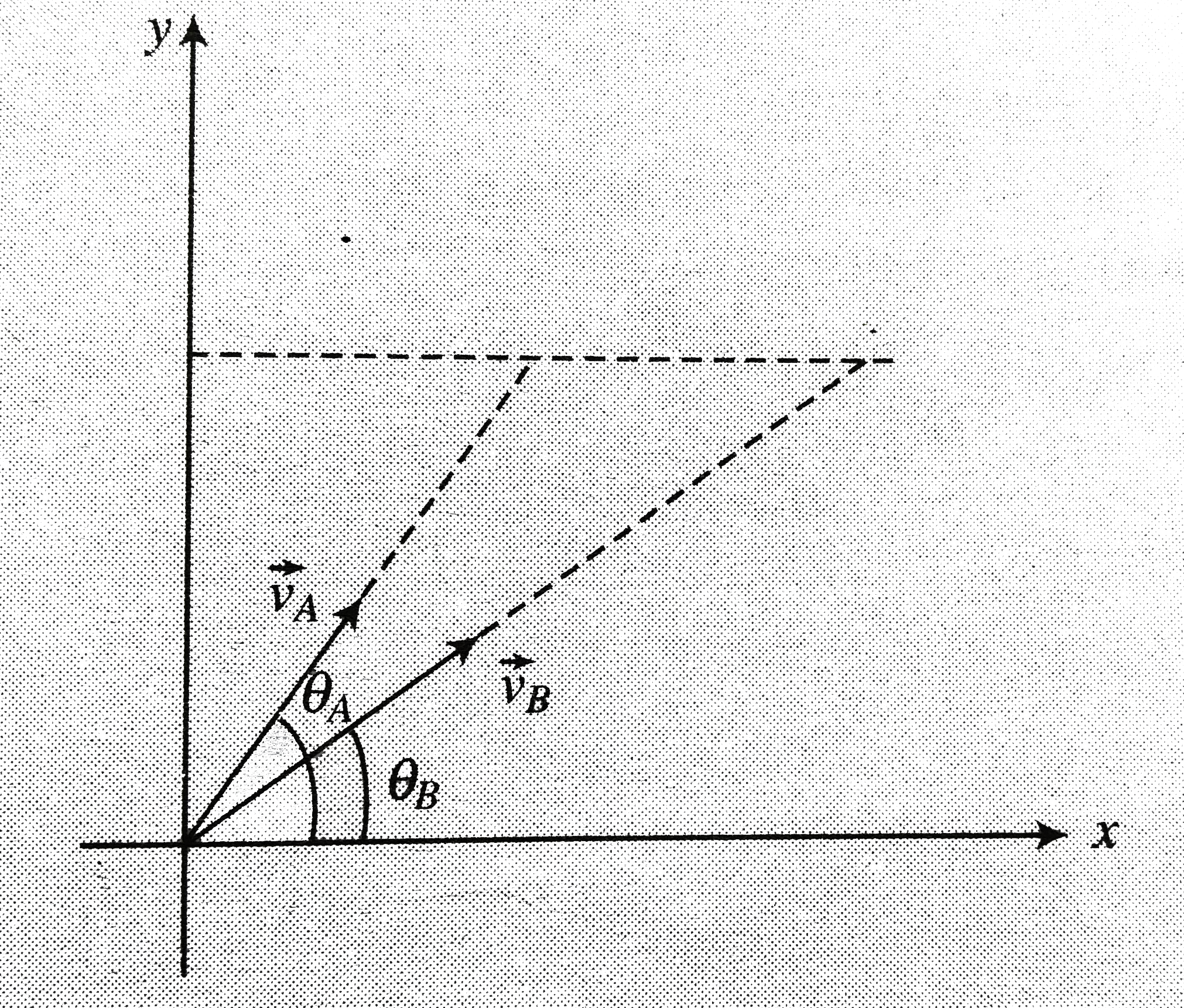 .
.
View SolutionTwo particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
View SolutionA body is projected horizontally from the top of a tower with a velocity of 10m/s.If it hits the ground at an angle 45∘, then vertical component of velocity when it hits ground in m/s is
View SolutionA body is projected horizontally from the top of a tower with a velocity of 10m/s. If it hits the ground at an angle of 45∘, the vertical component of velocity when it hits ground in m/s is
View SolutionTwo particles are projected at the same instant from the same point at inclinations α and β to the horizontal. If they simultaneously hit the top and bottom of a vertical pole subtending angle θ at the point of projection , find (tanα−tanβ).
View SolutionTwo particles were projected one by one with the same initial velocity from the same point on level ground. They follow the same parabolic trajectory and are found to be in the same horizontal level, separated by a distance of 1m,2s after the second partice was projected. Assume that the horizontal component of their velocities is 0.5ms−1. Find
(a) the horizontal range of the parabolic path.
(b) the maximum height for the parabolic path.
View Solution
