The body moves along the x−axis . At time t=0 the velocity of particle is +0.5m/s. The acceleration of particle in different time interval is given as:
a=⎧⎪
⎪⎨⎪
⎪⎩−1m/s2 0s≤t≤3s−2m/s2 3s<t<6s+4m/s2 6s≤t≤10s
The speed of particle at t=6s is zero.
The speed of particle at t=6s is 6m/s.
The speed of particle of at t=10s is 25m/s
The speed of particle at t=10s is 12m/s.
The correct Answer is:D
To solve the problem, we will calculate the velocity of the particle at different time intervals using the given acceleration values.
1. Initial Conditions:
- At time t=0, the initial velocity u=0.5m/s.
2. Acceleration from t=0 to t=3 seconds:
- Given acceleration a=−1m/s2.
- Using the formula v=u+at:
v(3)=0.5+(−1)×3
v(3)=0.5−3=−2.5m/s
3. Acceleration from t=3 to t=6 seconds:
- Now, the new initial velocity u=−2.5m/s and acceleration a=−2m/s2.
- Again using the formula v=u+at:
v(6)=−2.5+(−2)×3
v(6)=−2.5−6=−8.5m/s
4. Acceleration from t=6 to t=10 seconds:
- Now, the new initial velocity u=−8.5m/s and acceleration a=+4m/s2.
- Using the formula v=u+at:
v(10)=−8.5+4×4
v(10)=−8.5+16=7.5m/s
5. Final Result:
- The velocity of the particle at t=10 seconds is 7.5m/s.
Summary of Results:
- The calculated velocity of the particle at t=10 seconds is 7.5m/s.
- At time t=0, the initial velocity u=0.5m/s.
- Given acceleration a=−1m/s2.
- Using the formula v=u+at:
v(3)=0.5+(−1)×3
v(3)=0.5−3=−2.5m/s
- Now, the new initial velocity u=−2.5m/s and acceleration a=−2m/s2.
- Again using the formula v=u+at:
v(6)=−2.5+(−2)×3
v(6)=−2.5−6=−8.5m/s
- Now, the new initial velocity u=−8.5m/s and acceleration a=+4m/s2.
- Using the formula v=u+at:
v(10)=−8.5+4×4
v(10)=−8.5+16=7.5m/s
- The velocity of the particle at t=10 seconds is 7.5m/s.
- The calculated velocity of the particle at t=10 seconds is 7.5m/s.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - Exercise (Physics)
330 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Velocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The velocity of the body at time t = 3s is
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
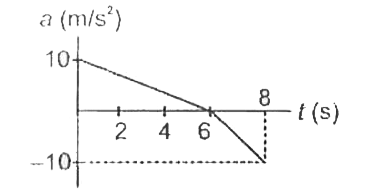
View SolutionA particle is moving eastwards with velocity of 5m/s. In 10sec the velocity changes to 5m/s northwards. The average acceleration in this time is.
View SolutionAt time t=0, a particle is at (−1m,2m) and at t=2s it is at (−4m,6m). From this we can conclude that in the given time interval.
View SolutionA particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.
View SolutionA particle moves in a straight line with constant speed of 4m/s for 2s, then with 6m/s for 3s. Find the average speed of the particle in the given time interval.
View SolutionA particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v=(10+5t−t2) At time t=0,x=0. Find
(a) acceleration of particle at t=2s and
(b) x-coordinate of particle at t=3s
View Solution
