Assertion:− The trajectory of projectile in XY plane is quadratic in x and linear in y if x is independent of X−coordinate.
Reason :− y−coordinate of trajetory is independent of x−coordinate.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertiion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are False
The correct Answer is:C
To solve the problem, we need to analyze both the assertion and the reason provided in the question.
1. Understanding the Assertion:
The assertion states that the trajectory of a projectile in the XY plane is quadratic in x and linear in y if x is independent of the x-coordinate.
- The trajectory of a projectile is generally described by the equations:
x=uxt
y=uyt−12gt2
where ux and uy are the horizontal and vertical components of the initial velocity, and g is the acceleration due to gravity.
2. Finding the Relationship:
- From the equation for x, we can express time t as:
t=xux
- Substituting this expression for t into the equation for y:
y=uy(xux)−12g(xux)2
- Simplifying this gives:
y=uyuxx−g2u2xx2
- This shows that y is a quadratic function of x (since it includes an x2 term) and thus confirms that the trajectory is quadratic in x.
3. Understanding the Reason:
- The reason states that the y-coordinate of the trajectory is independent of the x-coordinate.
- However, from our earlier derivation, we see that y is actually dependent on x because y is expressed as a function of x.
4. Conclusion:
- The assertion is true because the trajectory is indeed quadratic in x.
- The reason is false because the y-coordinate is dependent on the x-coordinate.
Final Answer:
- Assertion: True
- Reason: False
- Therefore, the correct option is that the assertion is true and the reason is false.
The assertion states that the trajectory of a projectile in the XY plane is quadratic in x and linear in y if x is independent of the x-coordinate.
- The trajectory of a projectile is generally described by the equations:
x=uxt
y=uyt−12gt2
where ux and uy are the horizontal and vertical components of the initial velocity, and g is the acceleration due to gravity.
- From the equation for x, we can express time t as:
t=xux
- Substituting this expression for t into the equation for y:
y=uy(xux)−12g(xux)2
- Simplifying this gives:
y=uyuxx−g2u2xx2
- This shows that y is a quadratic function of x (since it includes an x2 term) and thus confirms that the trajectory is quadratic in x.
- The reason states that the y-coordinate of the trajectory is independent of the x-coordinate.
- However, from our earlier derivation, we see that y is actually dependent on x because y is expressed as a function of x.
- The assertion is true because the trajectory is indeed quadratic in x.
- The reason is false because the y-coordinate is dependent on the x-coordinate.
- Assertion: True
- Reason: False
- Therefore, the correct option is that the assertion is true and the reason is false.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - Exercise (Physics)
330 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-
View SolutionSee Fig. 3.11 and complete the following statements:(i) The abscissa and the ordinate of the point B are _and _ Hence, the coordinates of B are (__,__).(ii) The x–coordinate and the y–coordinate of the point M are _ and _ respectively. Hence, the coordinates of M are (__,__).(iii) The x–coordinate and the y–coordinate of the point L are _ and _ respectively. Hence, the coordinates of L are (__,__).(iv) The .r–coordinate and the y–coordinate of the point S are _ and _ respectively. Hence, the coordinates of S are (__,__).
View Solution
Knowledge Check
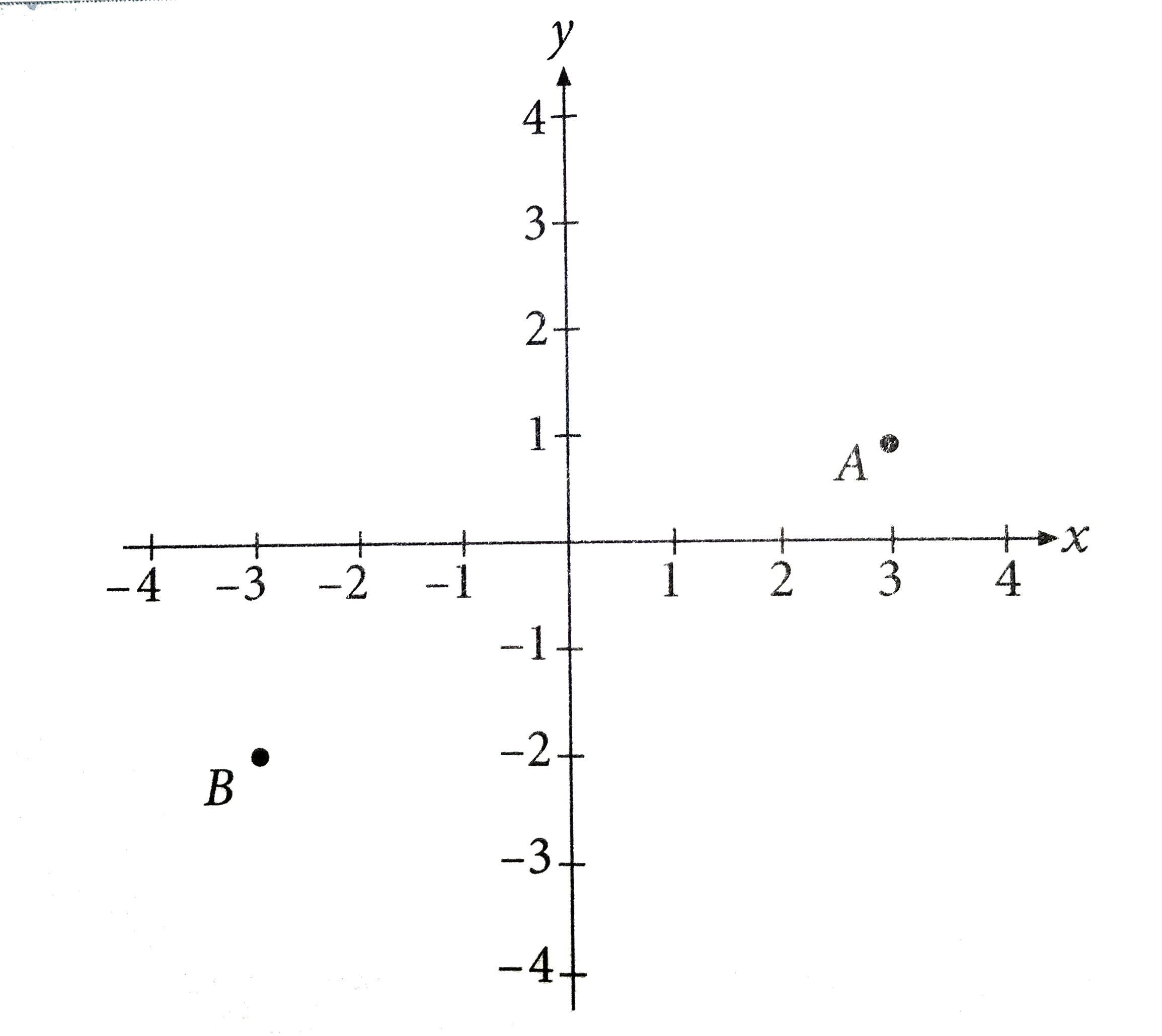
In the xy-plane above, what is the value of the x-coordinates of Point A minus the y-coordinates of Point B?A−2B−1C3D5The equation (x−7)2+(y−8)2=10 is that of a circle that lies in the standard (x,y) coordinate plane. One endpoint of a diameter of the circle has y-coordinate 11. What is the y-coordinate of the other endpoint of that diameter?
A1B3C4D5Which of the following is the equation of a circle in the standard (x,y) coordinate plane ?
A(x-3)+(y+6)=100By=x2+25Cx2=y2+25Dx2=36−y2
Find the slope of the tangent to curve y=x3−x+1 at the point whose x-coordinate is 2.
View SolutionThe line with the equation 45x+13y =1 is graphed in the xy‑plane. What is the x-coordinate of the x‑intercept of the line?
View SolutionIf a point lies on X-axis, then what are its y and z co-ordinates ?
View Solutionx coordinates of two points B and C are the roots of equation x2+4x+3=0 and their y coordinates are the roots of equation x2−x−6=0. If x coordinate of B is less than the x coordinate of C and y coordinate of B is greater than the y coordinate of C and coordinates of a third point A be (3,−5), find the length of the bisector of the interior angle at A.
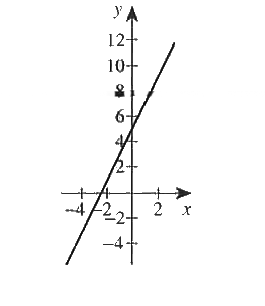
View SolutionOne of the following is an equation of the linear relation shown in the standard (x, y) coordinate plane below. Which equation is it?
View Solution
