Two forces f1=4N and f2=3N are acting on a particle along positve X−axis and negative y−axis respectively. The resultant force on the particle will be−
3ˆi+4ˆj
4ˆi+3ˆj
4ˆi−3ˆj
3ˆi−4ˆj
The correct Answer is:C
To find the resultant force acting on the particle due to the two forces F1 and F2, we can follow these steps:
Step 1: Identify the forces and their directions
- The first force F1=4N is acting along the positive x-axis.
- The second force F2=3N is acting along the negative y-axis.
Step 2: Represent the forces as vectors
- The force F1 can be represented as a vector:
F1=4^i
- The force F2 can be represented as a vector:
F2=−3^j
Step 3: Calculate the resultant force
- The resultant force FR is the vector sum of F1 and F2:
FR=F1+F2=4^i+(−3^j)=4^i−3^j
Step 4: Write the final expression for the resultant force
- Therefore, the resultant force acting on the particle is:
FR=4^i−3^j
- The first force F1=4N is acting along the positive x-axis.
- The second force F2=3N is acting along the negative y-axis.
- The force F1 can be represented as a vector:
F1=4^i
- The force F2 can be represented as a vector:
F2=−3^j
- The resultant force FR is the vector sum of F1 and F2:
FR=F1+F2=4^i+(−3^j)=4^i−3^j
- Therefore, the resultant force acting on the particle is:
FR=4^i−3^j
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
Two forces F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is
View SolutionTwo forces F1=1N and F2=2N act along the lines x=0 and y=0, respectively. Then find the resultant of forces.
View SolutionAccording to Newton.s second law of motion, resultant force on a particle is in the direction of acceleration of the particle. Two forcce F1andF2 are acting on a particle as shown in the figure. The acceleration of the particle is along X-axis. FInd the value of F1 (in newton)
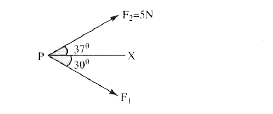
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View SolutionTwo force F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is :-
View SolutionA particle moves on a circular path of radius R under the action of two constant forces F1andF2.F1 act along positive x axis and F2 acts along positive y-axis. Find the work done by F1andF2 in moving the particle from position A to position B as shown in figure.
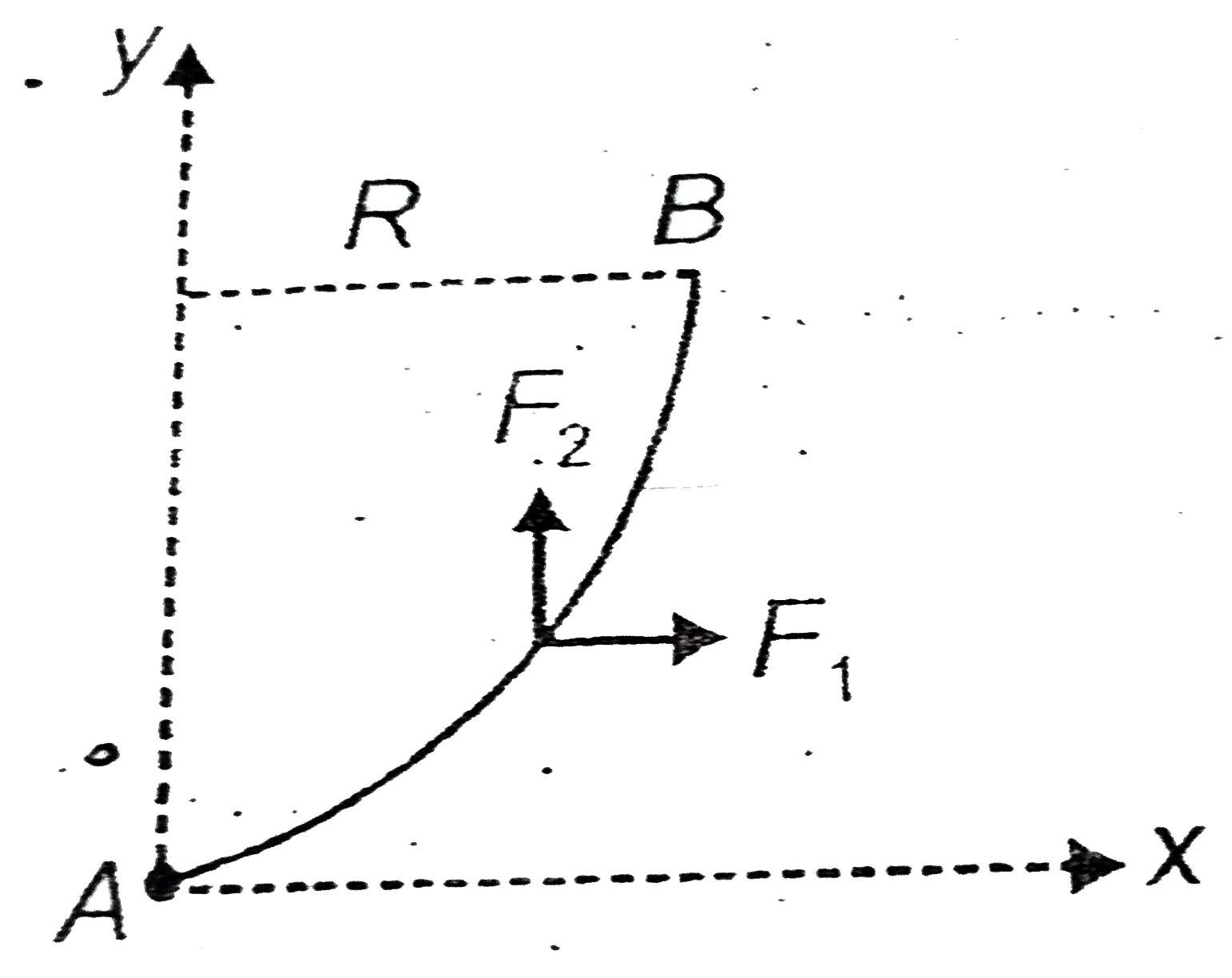
View SolutionForces F1andF2 act on a point mass in two mutually perpendicular directions. The resultant force on the point mass will be
View SolutionForces F1andF2 act on a point mass in two mutually perpendicular directions. The resultant force on the point mass will be
View SolutionTwo forces whose magnitudes are 2N and 3N act on a particle in the direction of the vectros 2ˆi+4ˆj+4ˆkand4ˆi−4ˆj+2ˆk respectively. If the particle is displaced from the origin O to the point (1,2,2). Find the work done.
View SolutionA single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
View Solution
