A single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
Wave number
Wavelength
Wave velocity
All of these
To solve the problem, we need to analyze the relationship between the torque, the position vector, and the force vector acting on a particle located on the negative x-axis.
1. Identify the Position Vector:
The particle is situated on the negative x-axis. Therefore, the position vector r can be expressed as:
r=−x^i
where x>0.
2. Understand the Torque Direction:
The problem states that the torque τ about the origin is in the positive z-direction. This can be represented as:
τ=τ^k
where τ is a positive scalar.
3. Torque Definition:
Torque is defined as the cross product of the position vector and the force vector:
τ=r×F
4. Set Up the Cross Product:
Substituting the position vector into the torque equation, we have:
τ^k=(−x^i)×F
5. Express the Force Vector:
Let the force vector F be expressed in terms of its components:
F=Fx^i+Fy^j+Fz^k
6. Calculate the Cross Product:
The cross product (−x^i)×(Fx^i+Fy^j+Fz^k) simplifies to:
τ=−x^i×(Fx^i)−x^i×(Fy^j)−x^i×(Fz^k)
The first term is zero since ^i×^i=0. The second term gives:
−x(−Fy)^k=xFy^k
The third term gives:
−x(−Fz^j)=−xFz^j
7. Equate to Torque:
Since the torque is in the positive z-direction, we have:
τ^k=xFy^k
This implies:
Fy=τx
8. Determine the Direction of Force:
The force must act in the negative y-direction to produce a positive torque in the z-direction. Thus, we conclude:
Fy<0(Force is in the negative y-direction)
Final Answer:
The force acting on the particle is directed in the negative y-direction.
---
The particle is situated on the negative x-axis. Therefore, the position vector r can be expressed as:
r=−x^i
where x>0.
The problem states that the torque τ about the origin is in the positive z-direction. This can be represented as:
τ=τ^k
where τ is a positive scalar.
Torque is defined as the cross product of the position vector and the force vector:
τ=r×F
Substituting the position vector into the torque equation, we have:
τ^k=(−x^i)×F
Let the force vector F be expressed in terms of its components:
F=Fx^i+Fy^j+Fz^k
The cross product (−x^i)×(Fx^i+Fy^j+Fz^k) simplifies to:
τ=−x^i×(Fx^i)−x^i×(Fy^j)−x^i×(Fz^k)
The first term is zero since ^i×^i=0. The second term gives:
−x(−Fy)^k=xFy^k
The third term gives:
−x(−Fz^j)=−xFz^j
Since the torque is in the positive z-direction, we have:
τ^k=xFy^k
This implies:
Fy=τx
The force must act in the negative y-direction to produce a positive torque in the z-direction. Thus, we conclude:
Fy<0(Force is in the negative y-direction)
The force acting on the particle is directed in the negative y-direction.
Topper's Solved these Questions
Similar Questions
A conservative force acts on a particle as the particle moves along the positive x-axis from origin origin to x=2m. The force is parallel to x-axis. Now, consider four different cases, as shown in the figures, 1, 2, 3, and 4, where the forces is shown as a function of x. Rank the situations according to the change in potential energy associated with the force, least ( or most negative) to greatest ( or most positive).
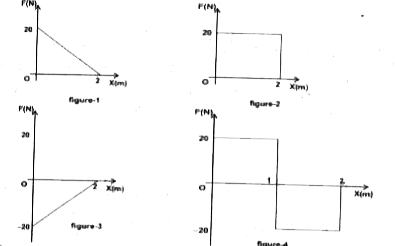
View SolutionOne of the forces acting on the particle is conservative, then
View Solution
Knowledge Check
Let →F be a force acting on a particle having positon vector →r.Let→τ be the torque of this force about the origin then
A→r.→τ>0 and →F.→τ<0B→r.→τ=0 and →F.→τ=0C→r.→τ=0 and →F.→τ≠0D→r.→τ≠0 and →F.→τ=0
A force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about origin?
View SolutionA force Fˆk acts on O, the origin of the coordinate system. The torque of this force about the point is: (1,−1) is
View SolutionA force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about the origin.
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View SolutionA force of −4Fˆk acts at O, the origin of the coordinate system. The torque about the point (1,−1) is
View SolutionOne of the forces acting on a particle is conservative then which of the following statement (s) are true about this conservative force
View Solution
