A neutral atom (A) is converted to (A) by the following process
AE1−−−→−e−1A+E2−−→e−A+2E3−−→e−A3+
The correct order of of E1, E2 and E3 energies is :−
E1<E2<E3
E1>E2>E3
E1=E2=E3
E1>E2<E3
The correct Answer is:A
To solve the problem, we need to analyze the process of removing electrons from a neutral atom (A) to form cations (A⁺, A²⁺, A³⁺) and determine the order of the ionization energies (E₁, E₂, E₃) involved in this process.
1. Understanding Ionization Energy:
- Ionization energy is the energy required to remove an electron from an atom or ion in its gaseous state.
- The first ionization energy (E₁) is the energy required to remove the most loosely bound electron from a neutral atom (A) to form a cation (A⁺).
- The second ionization energy (E₂) is the energy required to remove an electron from the cation (A⁺) to form a doubly charged cation (A²⁺).
- The third ionization energy (E₃) is the energy required to remove an electron from the doubly charged cation (A²⁺) to form a triply charged cation (A³⁺).
2. Analyzing the Trend:
- As we remove electrons from the atom, the positive charge on the remaining cation increases (from A to A⁺ to A²⁺ to A³⁺).
- With each successive removal of an electron, the effective nuclear charge experienced by the remaining electrons increases. This is because there are fewer electrons to shield the positive charge of the nucleus.
3. Comparing Ionization Energies:
- Due to the increased effective nuclear charge, the energy required to remove an electron from a cation is greater than that required to remove an electron from a neutral atom.
- Therefore, we can conclude:
- E₁ < E₂ < E₃
- This means that the first ionization energy (E₁) is the lowest, followed by the second (E₂), and the third (E₃) is the highest.
4. Final Order:
- The correct order of the ionization energies is:
- E₃ > E₂ > E₁
Answer:
The correct order of energies is: E₃ > E₂ > E₁.
- Ionization energy is the energy required to remove an electron from an atom or ion in its gaseous state.
- The first ionization energy (E₁) is the energy required to remove the most loosely bound electron from a neutral atom (A) to form a cation (A⁺).
- The second ionization energy (E₂) is the energy required to remove an electron from the cation (A⁺) to form a doubly charged cation (A²⁺).
- The third ionization energy (E₃) is the energy required to remove an electron from the doubly charged cation (A²⁺) to form a triply charged cation (A³⁺).
- As we remove electrons from the atom, the positive charge on the remaining cation increases (from A to A⁺ to A²⁺ to A³⁺).
- With each successive removal of an electron, the effective nuclear charge experienced by the remaining electrons increases. This is because there are fewer electrons to shield the positive charge of the nucleus.
- Due to the increased effective nuclear charge, the energy required to remove an electron from a cation is greater than that required to remove an electron from a neutral atom.
- Therefore, we can conclude:
- E₁ < E₂ < E₃
- This means that the first ionization energy (E₁) is the lowest, followed by the second (E₂), and the third (E₃) is the highest.
- The correct order of the ionization energies is:
- E₃ > E₂ > E₁
The correct order of energies is: E₃ > E₂ > E₁.
Similar Questions
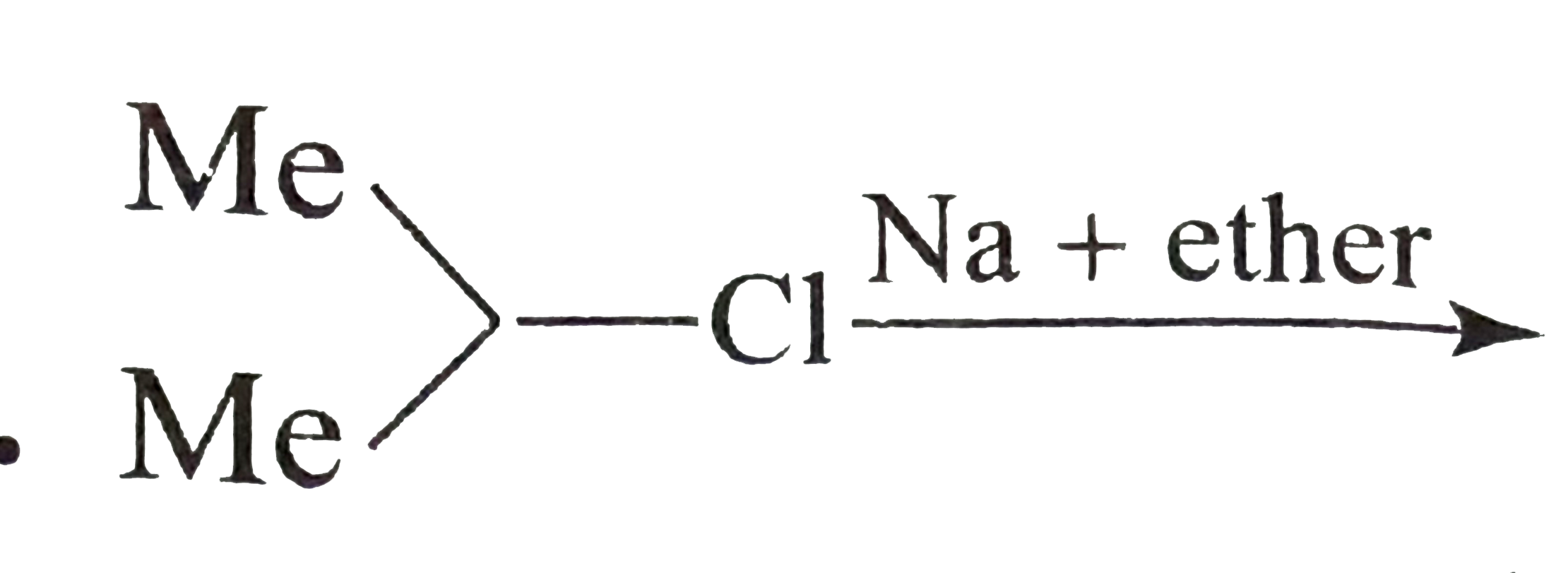 (B)2mol−−−−−−→Cl2+hv (C)2mol−−−−−−−−→Alc.KOH
(B)2mol−−−−−−→Cl2+hv (C)2mol−−−−−−−−→Alc.KOH
(D) CH2=CH2−−−−−−−→Δ (E)
The final product (E) is :
View SolutionConvert the following:
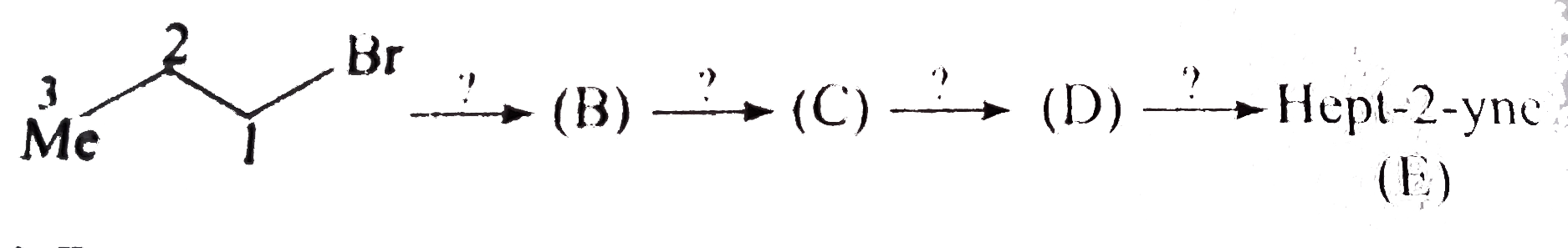 ?−−→(B)?−−→(C)?−−→(D)Hept-2-yne(E)
?−−→(B)?−−→(C)?−−→(D)Hept-2-yne(E)
1-Bromopropane (A)
View SolutionGiven 2∫1ex2dx=a, the value of e4∫e√logexdx, is
View SolutionComplete the following reactions:
Benzene(A) Ac2O−−−−→+AICI3 (B) (i)MeMgBr−−−−−−−→(ii)H3O(+) (C) Conc.H2SO4 (D) 1.BH3/THF−−−−−−−−−−→2.H2O2/O(−)H (E)
View Solutionπ/2∫−π/2cosx1+exdx=
View SolutionCH3−C∣∣O−H(1 e.q)+H−C∣∣O−HExcessOH−−−→ product
View Solution(a)
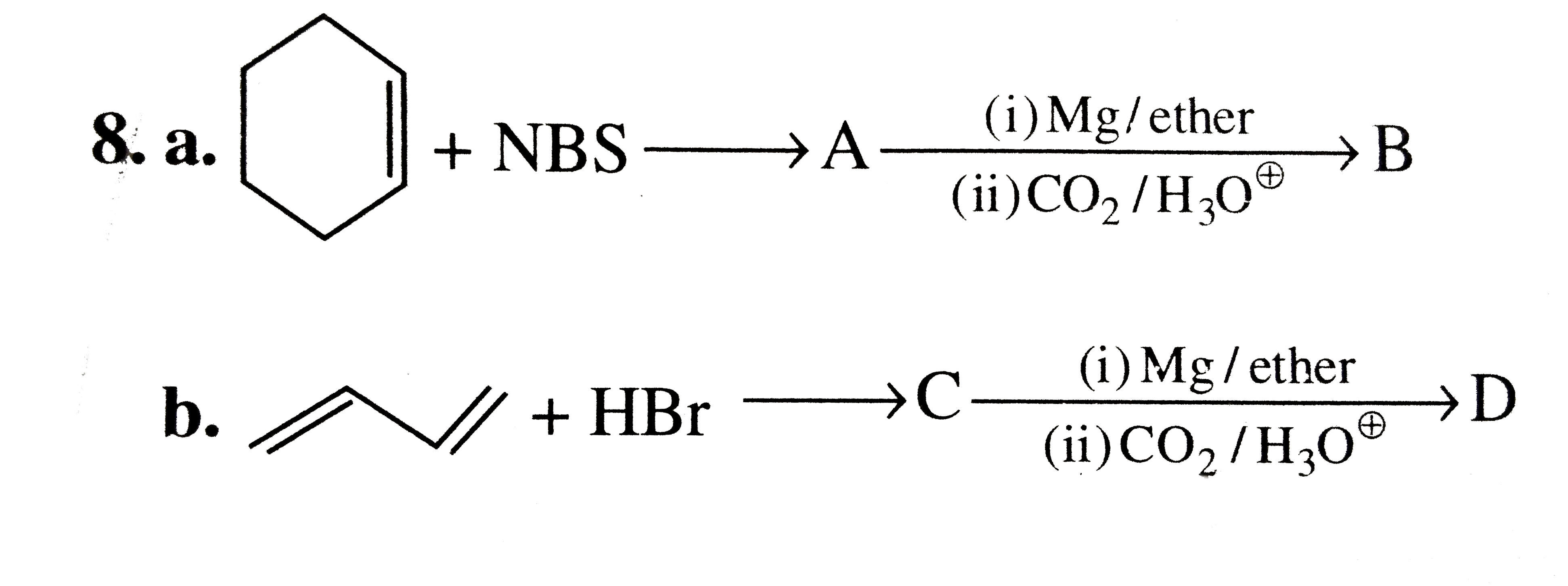
(b)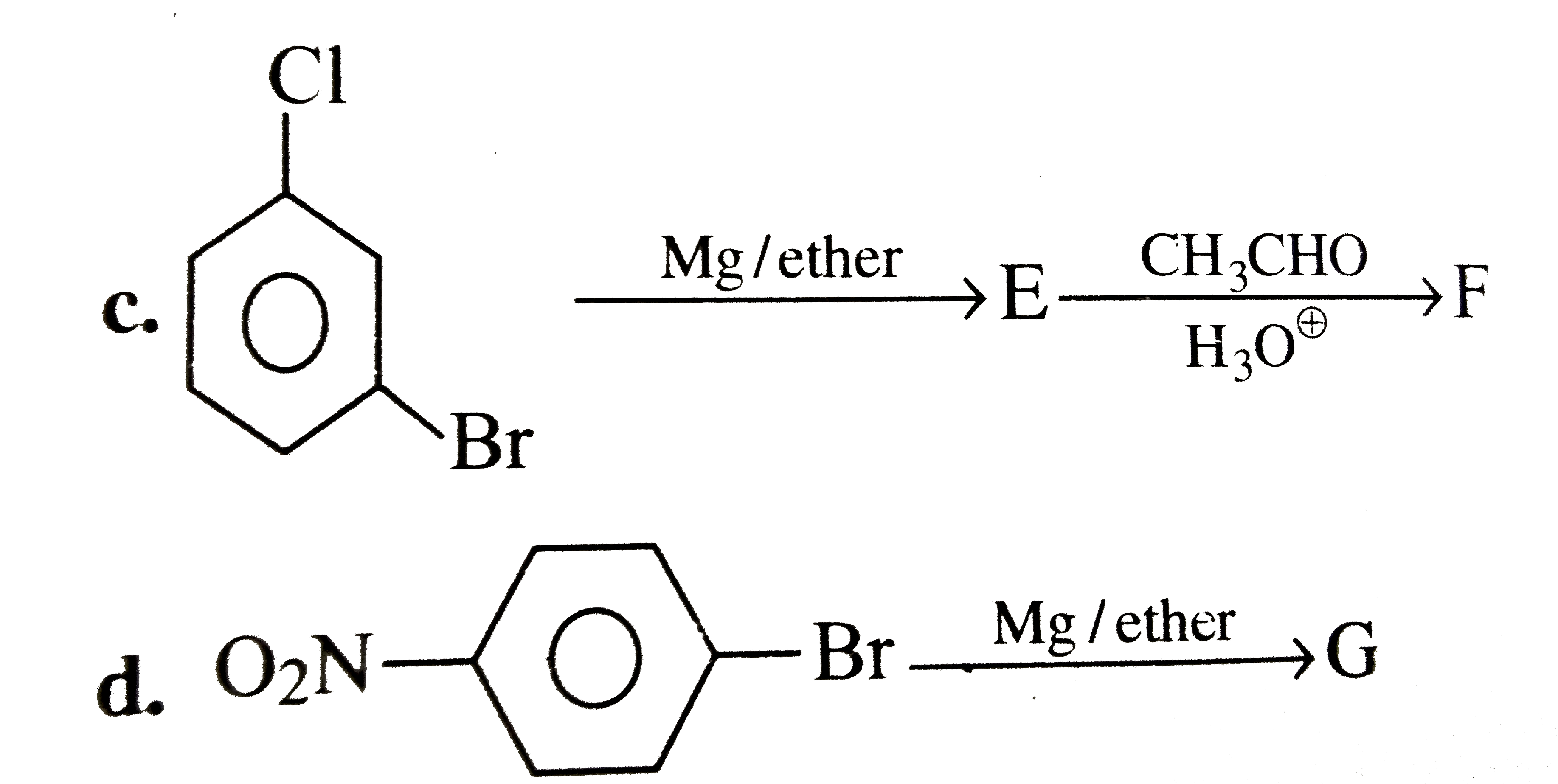
( e) PhMgBrO2−−−→H3O⊕?
(f) Phenol+RMgI→?.
View SolutionThe value of the integral e2∫e−1∣∣∣logexx∣∣∣dx is
View SolutionConsider the integrals
I1=1∫0e−xcos2xdx,I2=1∫0e−x2cos2xdx,I3=1∫0e−x2/2cos2xdx
and I4=1∫0e−x2/2dx. The greatest of these integrals, is
View SolutionThe value of the integral 1∫0ex2dx lies in the integral
View Solution
