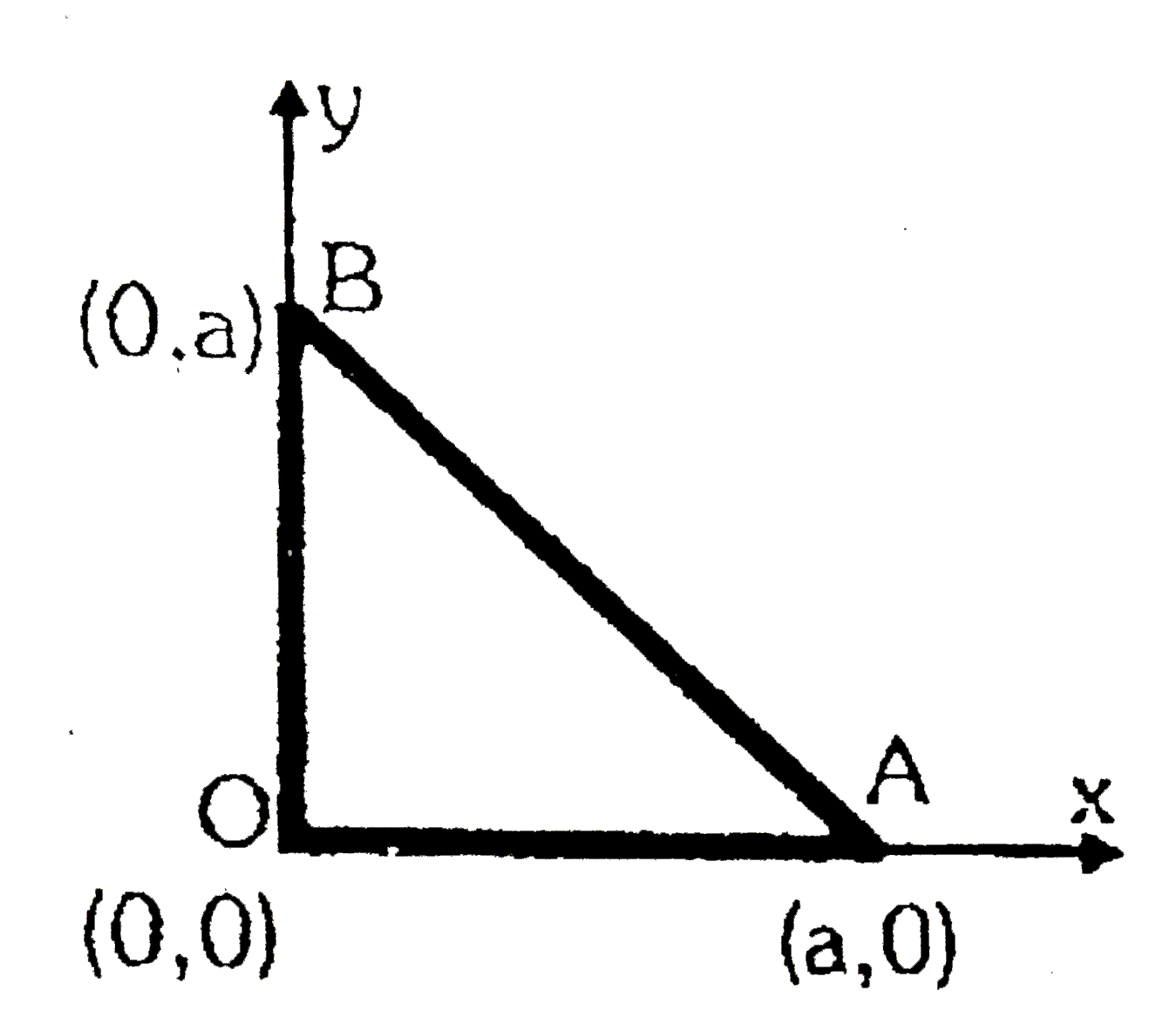
Three rods of the same mass are placed as shown in the figure. Calculate the coordinates of the centre of mass of the system.
(a3,a3)
(a2,a3)
(a3,a2)
(a2,a2)
The correct Answer is:A
Ans.(1)

Centre of Mass of rod OA is at (a2,0)
Centre of Mass of rod OB is (0,a2)
Centre of Mass of rod AB is (a2,a2)
For system Xcm=m×a2+m×0+m×a2m+m+m=a3
& Ycm=m×0+m×a2+m×a2m+m+m=a3
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
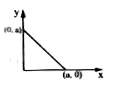
If three rods of same mass are placed as shown in the figure, the co-ordinates of the centre of mass of the system are
View SolutionCalculate centre of mass of the system
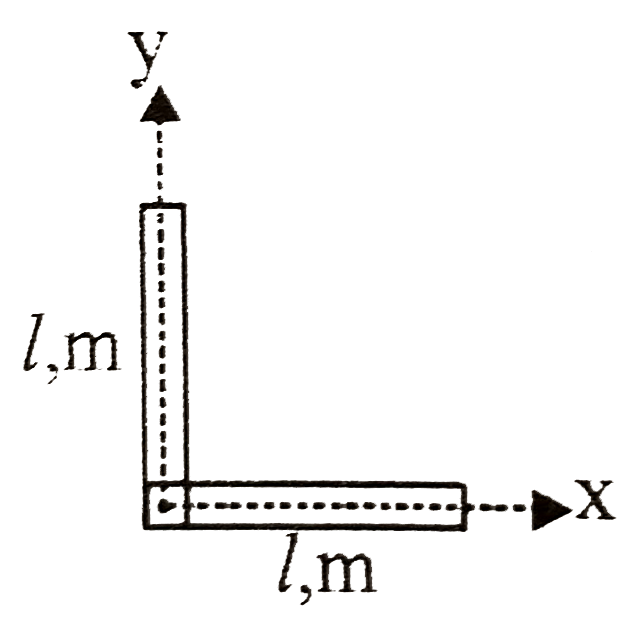
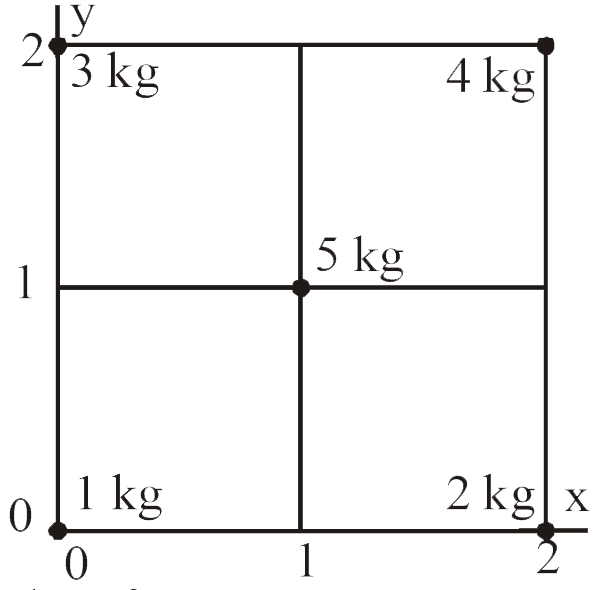
View SolutionFive masses are placed in a plane as shown in figure. The coordinates of the centre of mass are nearest to
View SolutionA uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
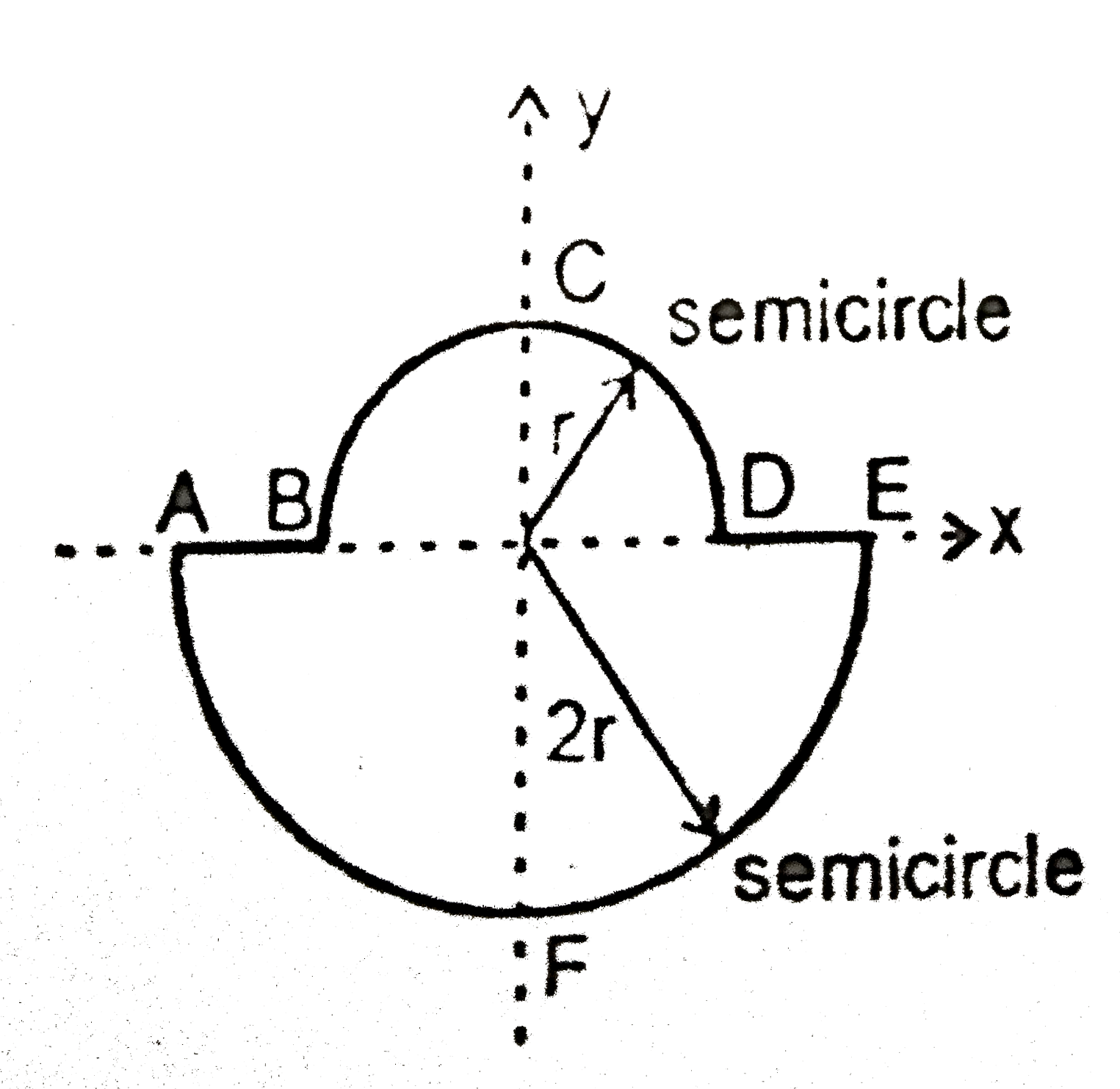
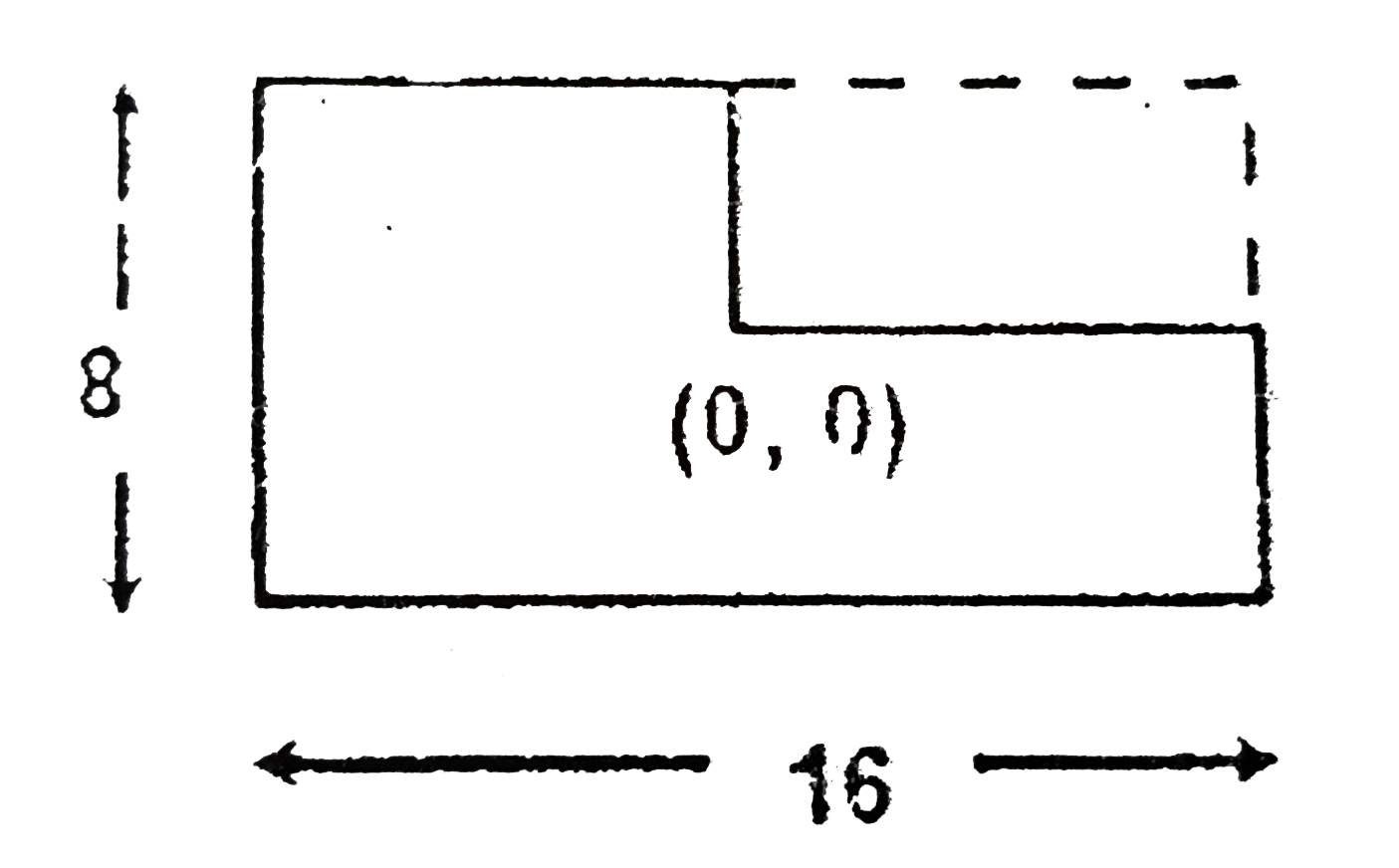
View SolutionFrom a 16cm×8cm rectangular uniform plane sheet, exactly one quarter of the sheet is removed as shown in figure. If the origin be taken at the centre of the sheet considered as shown in the figure the coordinates of the centre of mass of the remaining sheet is
View SolutionThe co-ordinates of the centre of mass of the system as shown in figure are
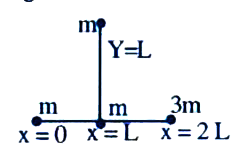
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

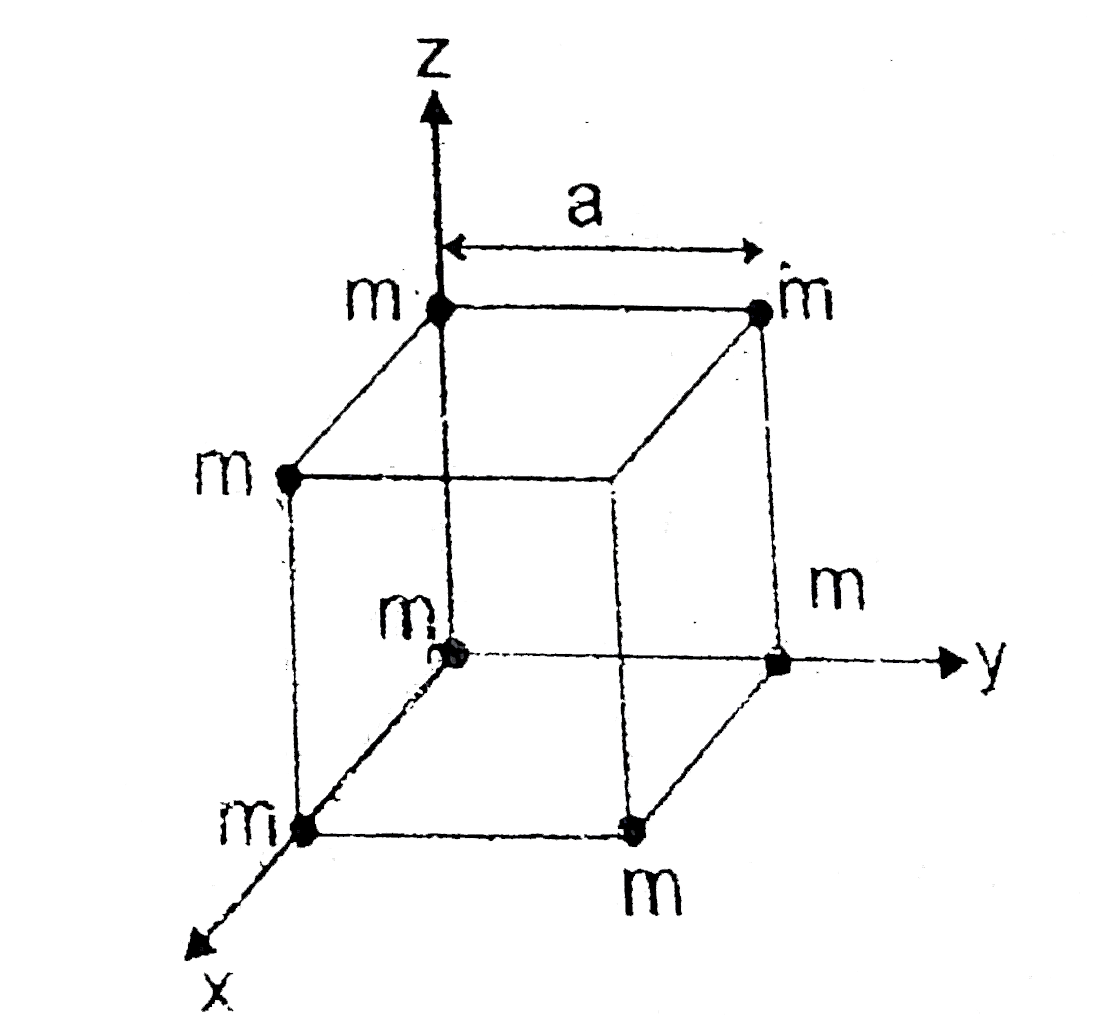
View SolutionSeven particles, each of mass m are placed at the seven corners of a cube of side 'a', but one corner is vacant, as shown in figure. If the x−coordinates of the centre of mass of the system is nam. Where n and m are least integer values. Then find vlaue of m−n.
View SolutionA rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
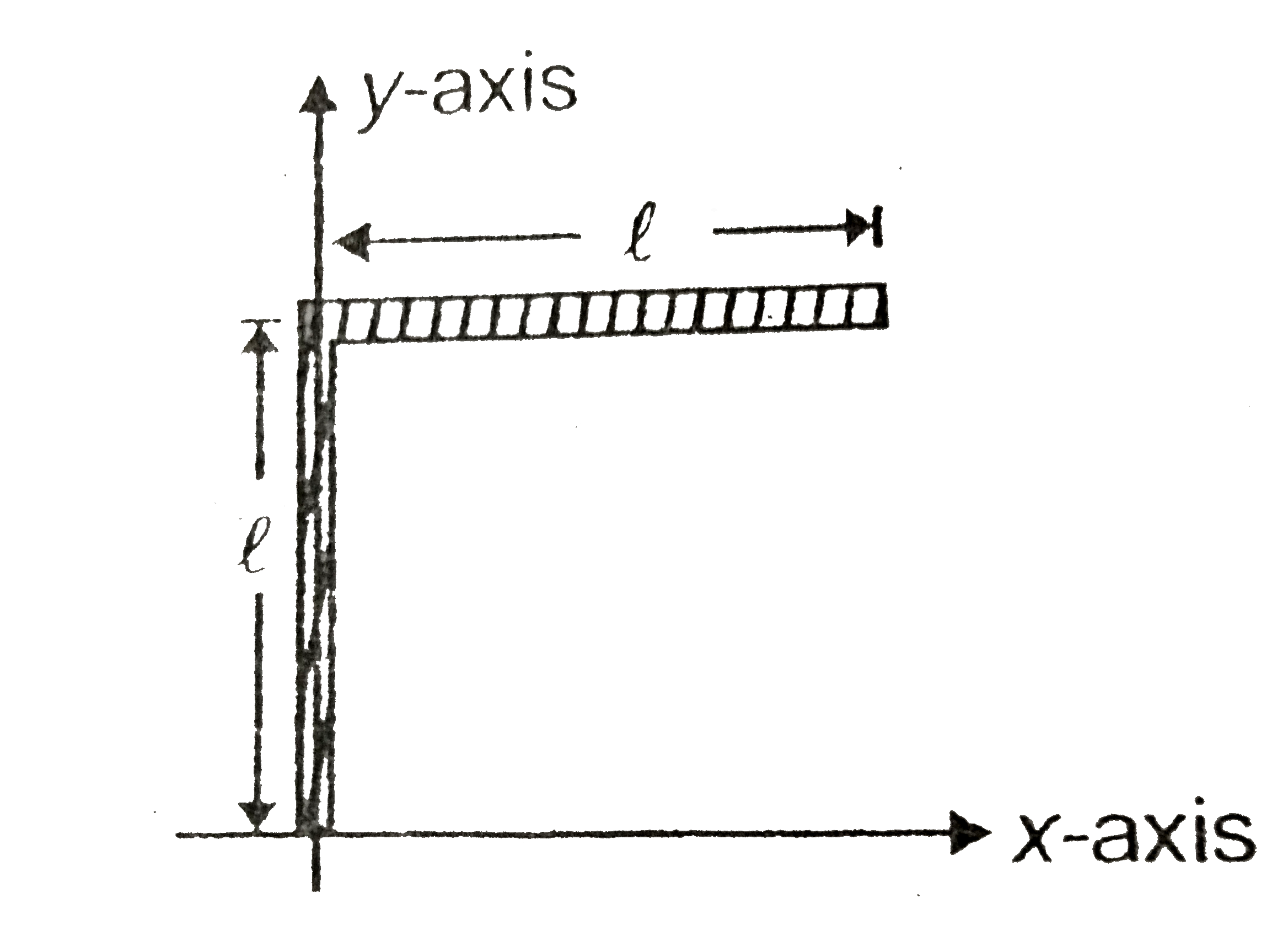
View SolutionThree particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png)
View Solution
