Arrange the following wavelenghts (λ)of given emission lines of H atoms in increasing order Choose the correct option (1) λ4<λ3<λ2<λ1 (2)λ4<λ2<λ3<λ1 (3) λ1<λ2<λ3<λ4 (4) λ1<λ3<λ2<λ4
n=3λ1−−→n=1
n=12λ3−−→n=10
n=5λ2−−→n=3
n=22λ4−−→n=20
The correct Answer is:C
To solve the problem of arranging the wavelengths of the given emission lines of hydrogen atoms in increasing order, we will follow these steps:
Step 1: Understand the Formula
The relationship between the wavelengths of the emission lines and the energy levels of the hydrogen atom is given by the formula:
1λ=RH(1n21−1n22)
where RH is the Rydberg constant, n1 is the lower energy level, and n2 is the higher energy level.
Step 2: Calculate Wavelengths
We will calculate the wavelengths for each transition:
1. For λ1 (Transition from 3 to 1):
1λ1=RH(112−132)=RH(1−19)=RH(89)
λ1=98RH
2. For λ2 (Transition from 5 to 3):
1λ2=RH(132−152)=RH(19−125)=RH(25−9225)=RH(16225)
λ2=22516RH
3. For λ3 (Transition from 12 to 10):
1λ3=RH(1102−1122)=RH(1100−1144)=RH(144−10014400)=RH(4414400)
λ3=1440044RH=327.27RH
4. For λ4 (Transition from 22 to 20):
1λ4=RH(1202−1222)=RH(1400−1484)=RH(484−400193600)=RH(84193600)
λ4=19360084RH=2304.76RH
Step 3: Compare Wavelengths
Now we will compare the calculated wavelengths:
- λ1=98RH
- λ2=22516RH
- λ3=327.27RH
- λ4=2304.76RH
Step 4: Arrange in Increasing Order
From the calculations, we can see that:
- λ1<λ2<λ3<λ4
Thus, the correct order of wavelengths in increasing order is:
λ1<λ2<λ3<λ4
Final Answer
The correct option is (3) λ1<λ2<λ3<λ4.
---
The relationship between the wavelengths of the emission lines and the energy levels of the hydrogen atom is given by the formula:
1λ=RH(1n21−1n22)
where RH is the Rydberg constant, n1 is the lower energy level, and n2 is the higher energy level.
We will calculate the wavelengths for each transition:
1λ1=RH(112−132)=RH(1−19)=RH(89)
λ1=98RH
1λ2=RH(132−152)=RH(19−125)=RH(25−9225)=RH(16225)
λ2=22516RH
1λ3=RH(1102−1122)=RH(1100−1144)=RH(144−10014400)=RH(4414400)
λ3=1440044RH=327.27RH
1λ4=RH(1202−1222)=RH(1400−1484)=RH(484−400193600)=RH(84193600)
λ4=19360084RH=2304.76RH
Now we will compare the calculated wavelengths:
- λ1=98RH
- λ2=22516RH
- λ3=327.27RH
- λ4=2304.76RH
From the calculations, we can see that:
- λ1<λ2<λ3<λ4
λ1<λ2<λ3<λ4
The correct option is (3) λ1<λ2<λ3<λ4.
Topper's Solved these Questions
- CHEMISTRY AT A GLANCEBOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - INORGANIC CHEMISTRY
300 Videos
- CHEMISTRY AT A GLANCEBOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - ORGANIC CHEMISTRY
472 Videos
- Chemical EquilibriumBOOK - ALLENCHAPTER - Chemical EquilibriumEXERCISE - All Questions
30 Videos
- ELECTROCHEMISTRYBOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE -05 [B]
38 Videos
Similar Questions
Knowledge Check
If α,β are the roots of the equation λ(x2−x)+x+5=0 and if λ1andλ2 are two values of λ obtained from αβ+βα=4, then λ1λ22+λ2λ21 equals.
A4192B4144C4096D4048
If a1=a,a2=b,an+2=an+1+an2,n≥0 then limn→∞an is a+λ1bλ2,(λ1,λ2εI) where λ1+λ2 is _______
View SolutionThe wavelength of the first Lyman lines of hydrogen He+ and Li2+ ions and λ1,λ2&λ3 the ratio of these wavelengths is
View SolutionFind the values of λandμ if both the roots of the equation (3λ+1)x2=(2λ+3μ)x−3 are infinite.
View SolutionWithout using the tables , prove that
1log3λ+1log4λ>2 .
View Solution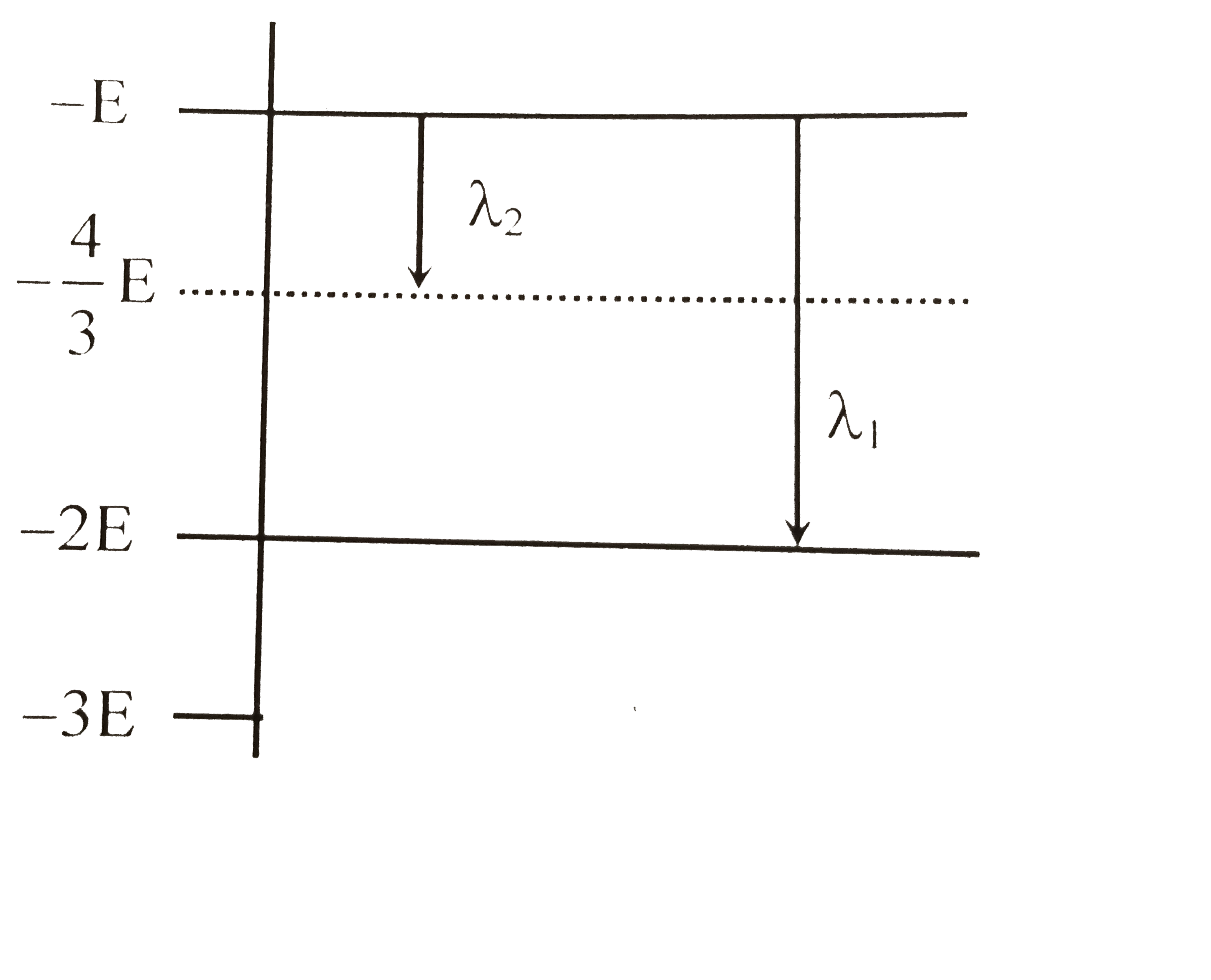
Some energy levels of a molecule are shown in the figure. The ratio of the wavelength r=λ1λ2,is given by:
View SolutionThe ration of resolving powers of an optical microscope for two wavelangths
λ1=4000 Åandλ2=6000Åis
View SolutionIf α,β are the roots fo the equation λ(x2−x)+x+5=0. If λ1 and λ2 are two values of λ for which the roots α,β are related by αβ+βα=45 find the value of λ1λ2+λ2λ1
View Solution
