When the value of (n + l) is not more than 3 which of the following subshell is not possible to exist?
2s
3s
3p
2p
The correct Answer is:C
To determine which subshell is not possible when the value of (n + l) is not more than 3, we will analyze the values of the principal quantum number (n) and the azimuthal quantum number (l).
1. Understanding Quantum Numbers:
- The principal quantum number (n) indicates the main energy level or shell.
- The azimuthal quantum number (l) indicates the subshell and can take values from 0 to (n - 1).
- The subshells correspond to values of l:
- l = 0 → s subshell
- l = 1 → p subshell
- l = 2 → d subshell
- l = 3 → f subshell
2. Setting Up the Condition:
- We need to find subshells for which (n + l) ≤ 3.
3. Case Analysis:
- Case 1: If (n + l) = 1
- The only possibility is n = 1, l = 0 → 1s subshell.
- Case 2: If (n + l) = 2
- Possible combinations:
- n = 2, l = 0 → 2s subshell.
- n = 1, l = 1 → Not possible since l can only be 0 when n = 1.
- Case 3: If (n + l) = 3
- Possible combinations:
- n = 3, l = 0 → 3s subshell.
- n = 2, l = 1 → 2p subshell.
- n = 1, l = 2 → Not possible since l can only be 0 or 1 when n = 1.
4. Identifying Possible Subshells:
- From the above cases, the possible subshells are:
- 1s (n=1, l=0)
- 2s (n=2, l=0)
- 2p (n=2, l=1)
- 3s (n=3, l=0)
5. Finding the Impossible Subshell:
- The subshells that cannot exist under the condition (n + l) ≤ 3 are:
- 3p (n=3, l=1) → This gives (3 + 1) = 4, which is greater than 3.
Conclusion:
The subshell that is not possible to exist when (n + l) is not more than 3 is 3p.
- The principal quantum number (n) indicates the main energy level or shell.
- The azimuthal quantum number (l) indicates the subshell and can take values from 0 to (n - 1).
- The subshells correspond to values of l:
- l = 0 → s subshell
- l = 1 → p subshell
- l = 2 → d subshell
- l = 3 → f subshell
- We need to find subshells for which (n + l) ≤ 3.
- Case 1: If (n + l) = 1
- The only possibility is n = 1, l = 0 → 1s subshell.
- Case 2: If (n + l) = 2
- Possible combinations:
- n = 2, l = 0 → 2s subshell.
- n = 1, l = 1 → Not possible since l can only be 0 when n = 1.
- Case 3: If (n + l) = 3
- Possible combinations:
- n = 3, l = 0 → 3s subshell.
- n = 2, l = 1 → 2p subshell.
- n = 1, l = 2 → Not possible since l can only be 0 or 1 when n = 1.
- From the above cases, the possible subshells are:
- 1s (n=1, l=0)
- 2s (n=2, l=0)
- 2p (n=2, l=1)
- 3s (n=3, l=0)
- The subshells that cannot exist under the condition (n + l) ≤ 3 are:
- 3p (n=3, l=1) → This gives (3 + 1) = 4, which is greater than 3.
The subshell that is not possible to exist when (n + l) is not more than 3 is 3p.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - INORGANIC CHEMISTRY300videos
CHEMISTRY AT A GLANCE
- BOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - ORGANIC CHEMISTRY472videos
CHEMISTRY AT A GLANCE
- BOOK - ALLENCHAPTER - Chemical EquilibriumEXERCISE - All Questions30videos
Chemical Equilibrium
- BOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE -05 [B]38videos
ELECTROCHEMISTRY
Similar Questions
Knowledge Check
- Question 1 - Select One
If (3x)2=81, which of the following is a possible value of x?
A2B3C6D9 - Question 2 - Select One or More
Which of the following alkenes are more stable than
 A
A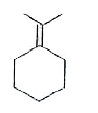 B
B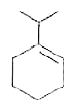 C
C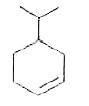 D
D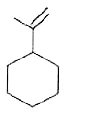
Which of the following alkene is more stable than
 View Solution
View SolutionIn which of the following pairs A is more stable than B?
View SolutionWhen is the value of van't Hoff factor more than one?
View SolutionWhich of the following is more basic than aniline?
View SolutionWhich of the following is more basic than aniline?
View SolutionWhich of the following is more basic than aniline? .
View Solution

