A block of 1 kg is stopped against a wall by applying a force F perpendicular to the wall. If μ=0.2 then minimum value of F will be
To solve the problem, we need to determine the minimum force F required to stop a block of mass 1kg against a wall, given that the coefficient of static friction μ=0.2.
1. Identify the Forces Acting on the Block:
- The weight of the block W=mg acts downwards, where m=1kg and g≈10m/s2.
- The applied force F acts perpendicular to the wall.
- The normal force N acts perpendicular to the wall due to the applied force F.
- The frictional force fs acts upwards, opposing the weight of the block.
2. Calculate the Weight of the Block:
W=mg=1kg×10m/s2=10N
3. Establish the Relationship Between Forces:
- The frictional force fs can be expressed as:
fs=μN
- Since the applied force F is equal to the normal force N (because F is perpendicular to the wall), we can write:
fs=μF
4. Set Up the Equilibrium Condition:
- For the block to be in equilibrium (not moving), the frictional force must balance the weight of the block:
fs=W
- Substituting the expression for fs:
μF=mg
5. Substitute Known Values:
- We know μ=0.2, m=1kg, and g≈10m/s2:
0.2F=10N
6. Solve for F:
F=10N0.2=50N
Final Answer:
The minimum value of the force F required to stop the block against the wall is 50N.
---
- The weight of the block W=mg acts downwards, where m=1kg and g≈10m/s2.
- The applied force F acts perpendicular to the wall.
- The normal force N acts perpendicular to the wall due to the applied force F.
- The frictional force fs acts upwards, opposing the weight of the block.
W=mg=1kg×10m/s2=10N
- The frictional force fs can be expressed as:
fs=μN
- Since the applied force F is equal to the normal force N (because F is perpendicular to the wall), we can write:
fs=μF
- For the block to be in equilibrium (not moving), the frictional force must balance the weight of the block:
fs=W
- Substituting the expression for fs:
μF=mg
- We know μ=0.2, m=1kg, and g≈10m/s2:
0.2F=10N
F=10N0.2=50N
The minimum value of the force F required to stop the block against the wall is 50N.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II
112 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
Similar Questions
A block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block weighs W is held against a vertical wall by applying a horizontal force F. The minimum value of F needed to hold the block is
View SolutionA block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass 'm' is held stationary against a rough wall by applying a force F as shown. Which one of the following statement is incorrect ?
A. Friction force = mg
B. F will not produce torque
C. Normal will not produce torque
D. Normal reaction = F
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA block of mass m is supported on a rough wall by applying a force in figure Coefficient of static friction between block and wall is μ
For what range of value of p , the block remain in static equilibrium ?

View SolutionA block of mass 5kg is held against a wall with a force of 100N. as shown om figure. It is moved horizontally slowly by applying a force parallel to the wall. Then the fricational force on the block due to wall is 25x newton. Find x. (Given μ=0.5 and g=10m/sec2)
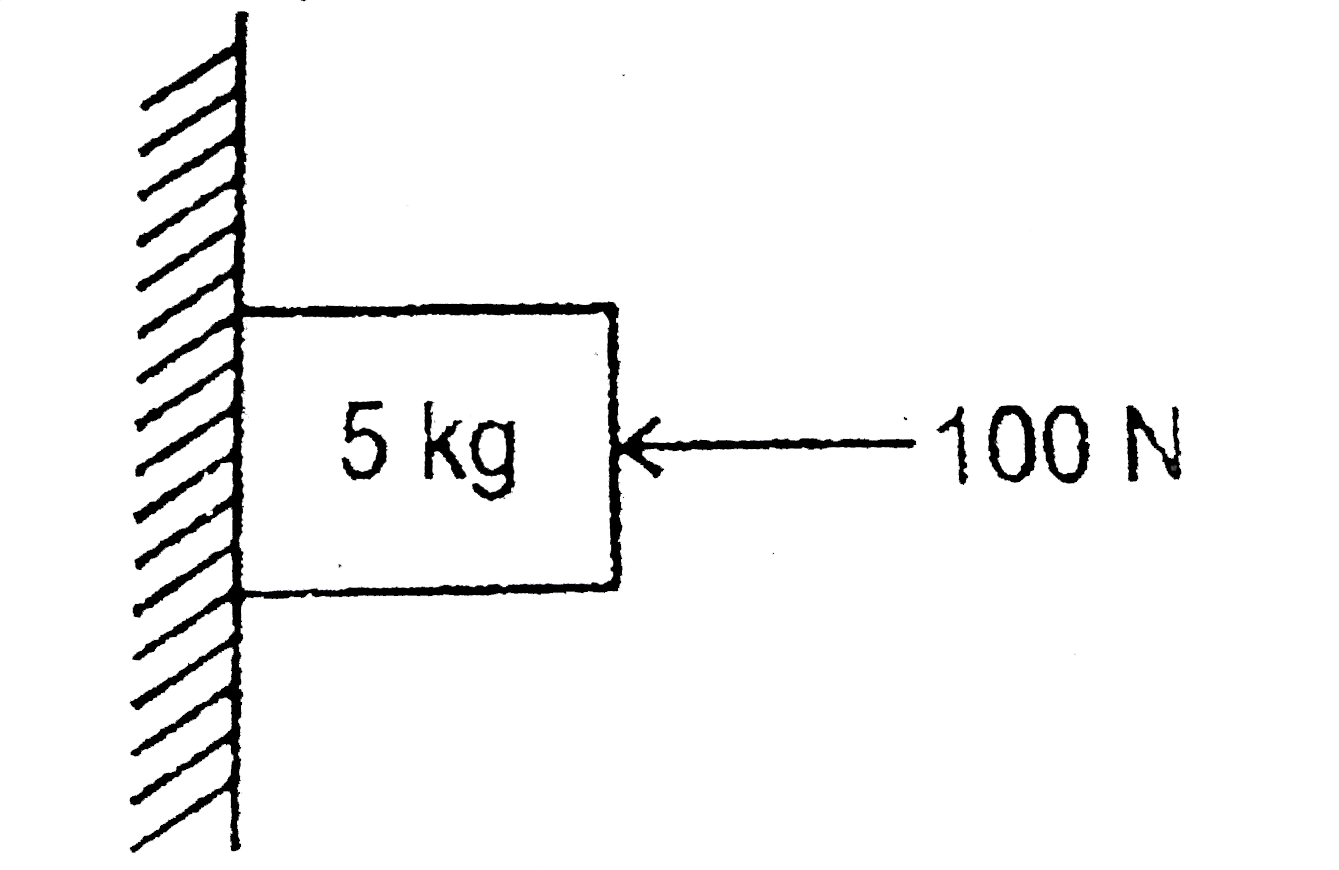
View Solution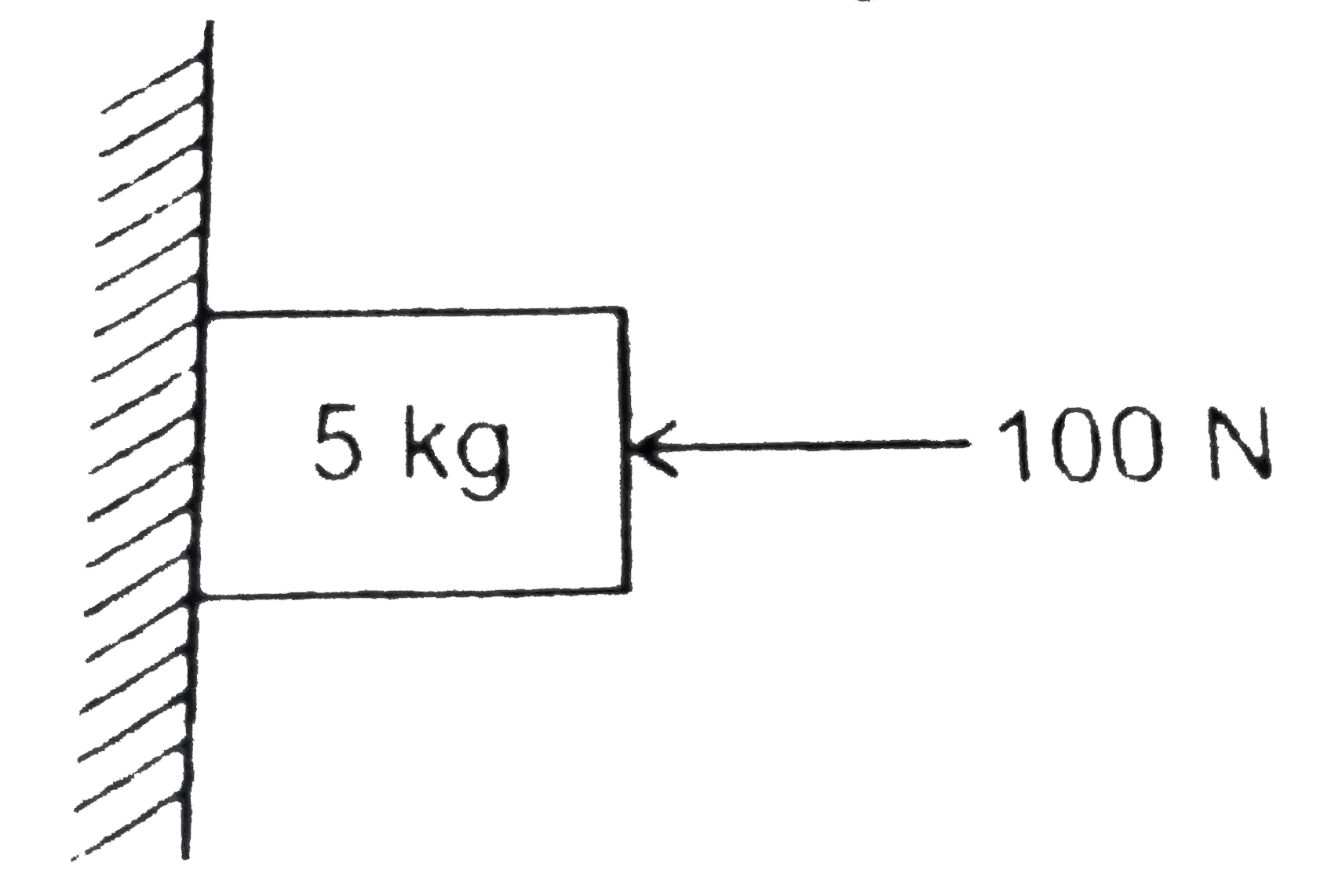
A block of mass 5 kg is held against a wall with a force of 100 N. as shown in figure. It is moved horizontally slowly by applying a force parallel to the wall. Thent he frictional force on the block due to wall is 25x newton find x. (given μ=0.5 and g=10msec2
View SolutionA block of mass 4kg pressed againest a rought wall by two perpendicular horizontal forces F1andF2as shown in figure Coefficient of static friction between the block and wall is 0.6 and that of kinetic friction is 0.5

For the data of Q 28 ,Find the magnitude of acceleration of the block
View SolutionA block of mass 4kg pressed againest a rought wall by two perpendicular horizontal forces F1=300NandF2=100Nas shown in figure Coefficient of static friction between the block and wall is 0.6 and that of kinetic friction is 0.5
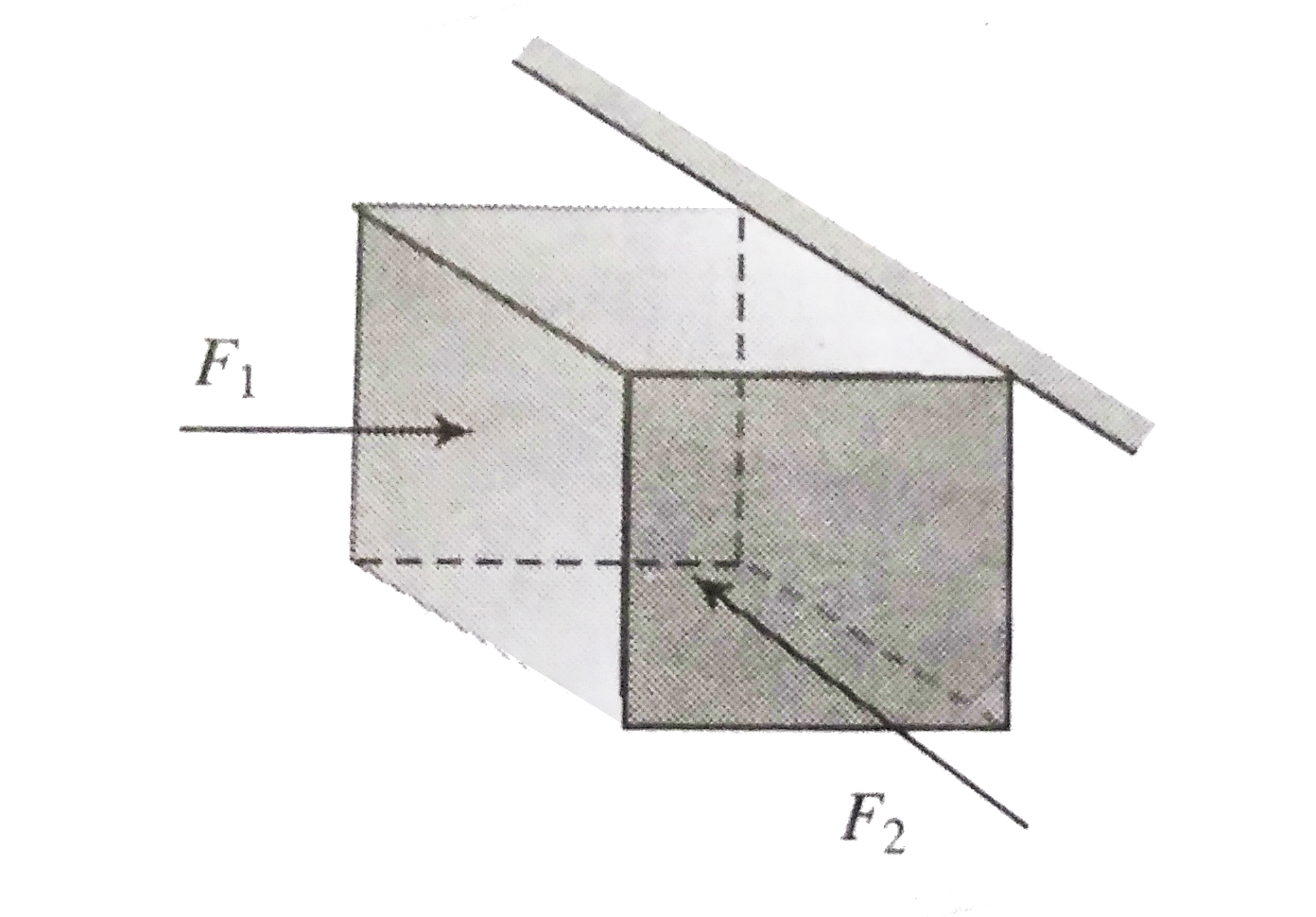
For the above data, what is the acceleration of block?
View Solution
