A block weighs W is held against a vertical wall by applying a horizontal force F. The minimum value of F needed to hold the block is
less tha W
Equal to W
Greater than W
Data is insufficient
The correct Answer is:C
To solve the problem of determining the minimum horizontal force F needed to hold a block weighing W against a vertical wall, we can analyze the forces acting on the block.
1. Identify the Forces Acting on the Block:
- The weight of the block W acts downward due to gravity.
- A horizontal force F is applied against the wall to hold the block in place.
- There is a frictional force f acting upward, which opposes the weight of the block.
2. Understanding the Role of Friction:
- The frictional force f can be expressed in terms of the normal force N exerted by the wall on the block. The relationship is given by:
f=μN
where μ is the coefficient of friction between the block and the wall.
3. Determine the Normal Force:
- In this scenario, the normal force N is equal to the applied horizontal force F since the wall is vertical and the force is applied horizontally. Thus, we have:
N=F
4. Equating Forces:
- For the block to remain stationary and not slide down the wall, the upward frictional force must balance the downward weight of the block. Therefore, we can write:
f=W
- Substituting the expression for friction, we get:
μF=W
5. Solving for the Minimum Force F:
- Rearranging the equation gives us:
F=Wμ
6. Analyzing the Coefficient of Friction:
- The coefficient of friction μ is a value that ranges between 0 and 1 (i.e., 0<μ<1). This means that:
F=Wμ>W
- Therefore, the minimum horizontal force F required to hold the block against the wall is greater than the weight of the block W.
Conclusion:
The minimum value of the horizontal force F needed to hold the block against the wall is greater than W.
Answer:
Option 3: Greater than W.
- The weight of the block W acts downward due to gravity.
- A horizontal force F is applied against the wall to hold the block in place.
- There is a frictional force f acting upward, which opposes the weight of the block.
- The frictional force f can be expressed in terms of the normal force N exerted by the wall on the block. The relationship is given by:
f=μN
where μ is the coefficient of friction between the block and the wall.
- In this scenario, the normal force N is equal to the applied horizontal force F since the wall is vertical and the force is applied horizontally. Thus, we have:
N=F
- For the block to remain stationary and not slide down the wall, the upward frictional force must balance the downward weight of the block. Therefore, we can write:
f=W
- Substituting the expression for friction, we get:
μF=W
- Rearranging the equation gives us:
F=Wμ
- The coefficient of friction μ is a value that ranges between 0 and 1 (i.e., 0<μ<1). This means that:
F=Wμ>W
- Therefore, the minimum horizontal force F required to hold the block against the wall is greater than the weight of the block W.
The minimum value of the horizontal force F needed to hold the block against the wall is greater than W.
Option 3: Greater than W.
Similar Questions
Minimum force F required to move the block
View SolutionA cubical block of side 'a' is held at rest, against a rough vertical wall by applying a force F acting along the centre. The mass of the block is m. Taking acceleration due to gravity as 'g' , determine
(i) The minimum coefficient of friction between the block and wall
(ii) The torque by normal reaction about the centre of mass
View Solution
Knowledge Check
A block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
AμMgBMgCMgμD2μMg
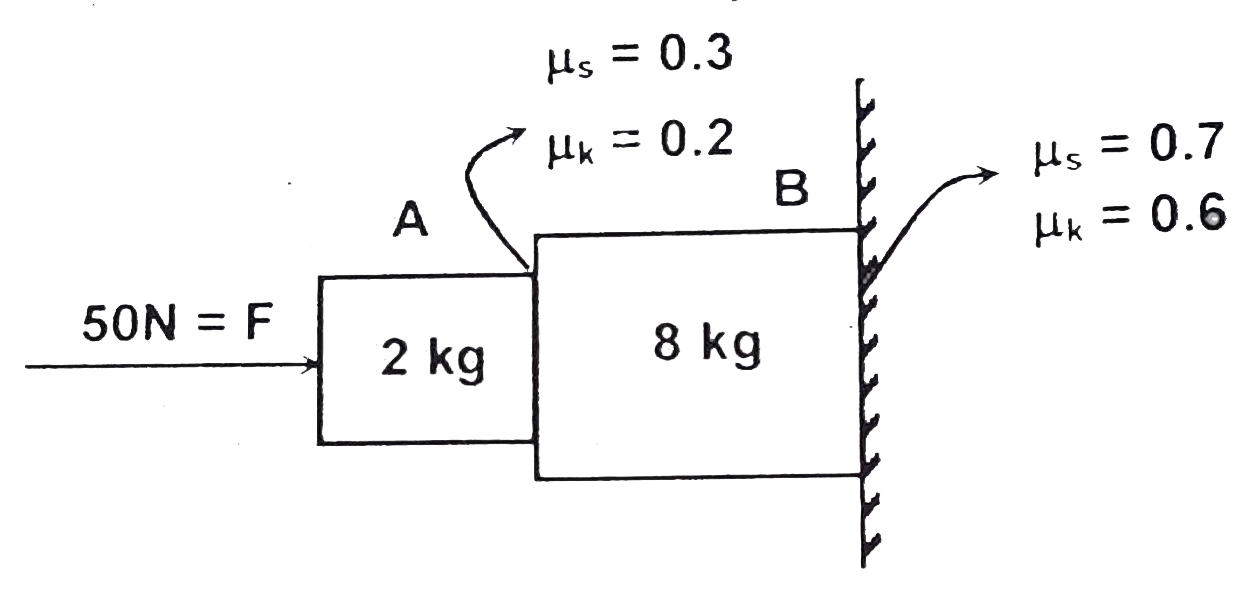
Two blocks A and B of masses 2kg and 8kg respectively are kept in contact and pressed against a roguh vertical wall by applying a horizontal force F=50N as shown, The frictional force acting between the two blocks is
View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
View SolutionA block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View Solution
