A marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
0.01
0.02
0.03
0.06
The correct Answer is:D
To solve the problem step by step, we will use the concepts of kinematics and friction.
Step 1: Identify the given values
- Mass of the marble block, m=2kg
- Initial velocity, u=6m/s
- Final velocity, v=0m/s (since the block stops)
- Time taken to stop, t=10s
Step 2: Use the kinematic equation
We can use the kinematic equation:
v=u+at
where a is the acceleration. Rearranging this gives:
a=v−ut
Step 3: Substitute the known values into the equation
Substituting the values we have:
a=0−610=−610=−0.6m/s2
The negative sign indicates that the acceleration is in the opposite direction of the initial velocity (deceleration).
Step 4: Relate acceleration to friction
The acceleration due to friction can also be expressed as:
a=−μg
where μ is the coefficient of friction and g is the acceleration due to gravity (approximately 10m/s2).
Step 5: Set the two expressions for acceleration equal
From the previous steps, we have:
−0.6=−μg
Substituting g=10m/s2:
−0.6=−μ⋅10
Step 6: Solve for the coefficient of friction μ
Rearranging gives:
μ=0.610=0.06
Conclusion
The coefficient of friction μ is 0.06.
---
- Mass of the marble block, m=2kg
- Initial velocity, u=6m/s
- Final velocity, v=0m/s (since the block stops)
- Time taken to stop, t=10s
We can use the kinematic equation:
v=u+at
where a is the acceleration. Rearranging this gives:
a=v−ut
Substituting the values we have:
a=0−610=−610=−0.6m/s2
The negative sign indicates that the acceleration is in the opposite direction of the initial velocity (deceleration).
The acceleration due to friction can also be expressed as:
a=−μg
where μ is the coefficient of friction and g is the acceleration due to gravity (approximately 10m/s2).
From the previous steps, we have:
−0.6=−μg
Substituting g=10m/s2:
−0.6=−μ⋅10
Rearranging gives:
μ=0.610=0.06
The coefficient of friction μ is 0.06.
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Match the columns
Explore 7 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
View SolutionA block slides on ice with a velocity of 5m/s comes to rest after moving through a distance of 13.5m . Find the coefficient of friction ?
View Solution
Knowledge Check
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
A man of mass 60 kg sitting on ice pushes a block of mass of 12kg on ice horizontally with a speed of 5 ms−1. The coefficient of friction between the man and ice and between block and ice is 0.2. If g =10 ms−2, the distances between man and the block, when they come to rest is
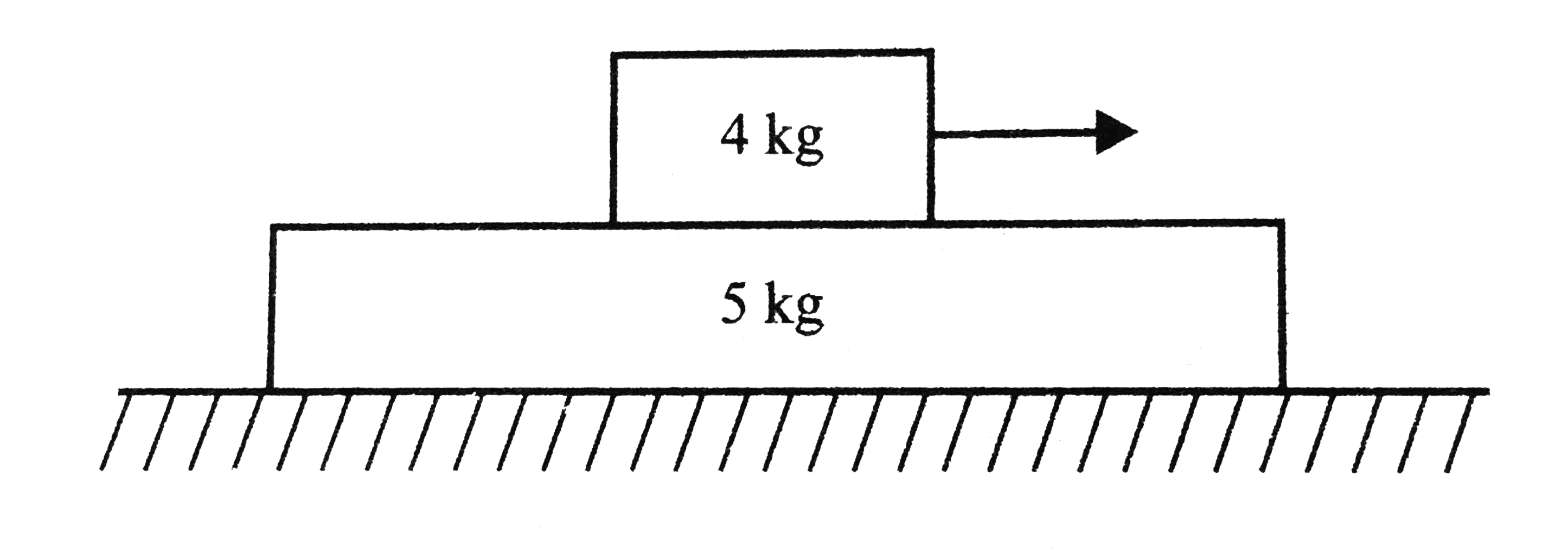
View SolutionA large slab of mass 5kg lies on a smooth horizontal surface, with a block of mass 4kg lying on the top of it. The coefficient of friction between the block and the slab is 0.25. If the block is pulled horizontally by a force of F =6N, the work done by the force of friction on the slab, between the instants t=2s and t=3s, is (g=10ms−2)
View SolutionA body of mass 10 kg moves on rough horizontal surface with initial velocity 10m/s and travels 500m before coming to rest. The coefficient of friction is
View SolutionA block of mass 5 kg slides down a rough inclined surface. The angle of inclination is 45∘. The coefficient of sliding friction is 0.20. When the block slides 10 cm, the work done on the block by force of friction is
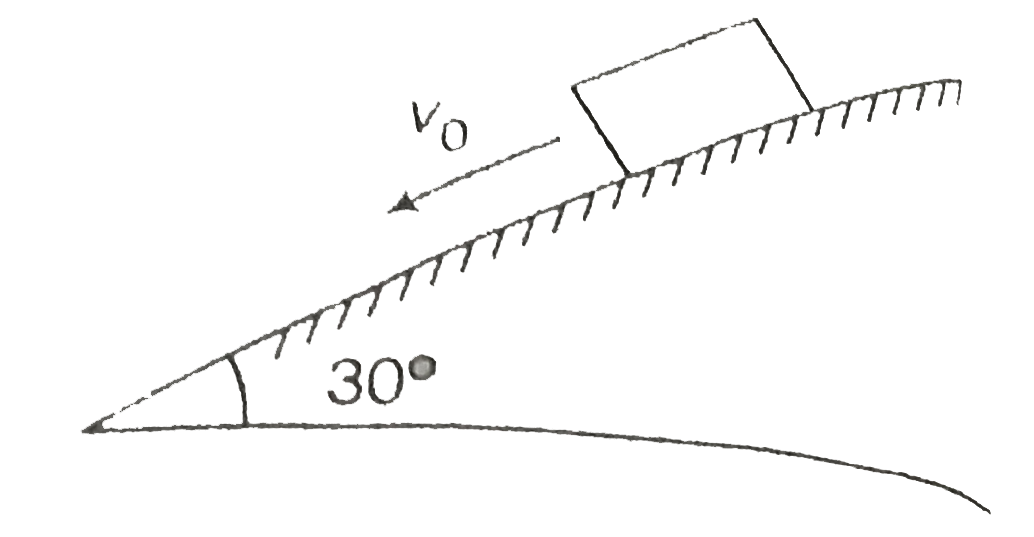
View SolutionA block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
View SolutionIn the given diagram, the block of mass 2 kg and 3 kg are placed one over the other . The contact surfaces are rough with coefficient of friction μ1=0.2,μ92)=0.06) . A force F=12t N ( where t is in second ) is applied on upper block in the direction ( Given that g = 10m/s2)
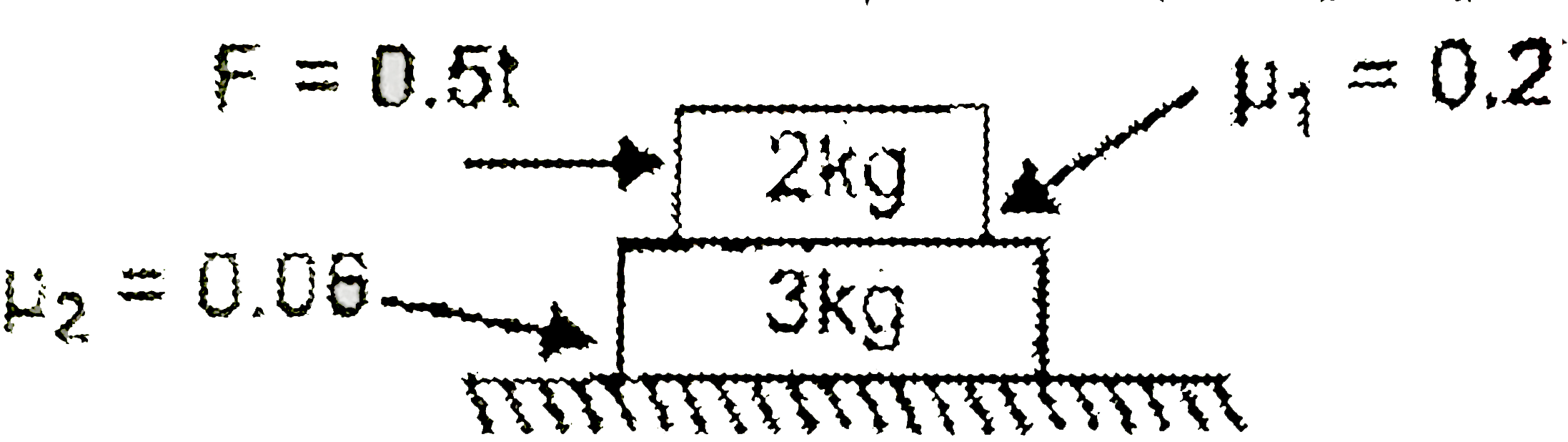
The acceleration time graph for 4 kg block is : Friction force acting between the two blocks at t=8 s
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View Solution