One mole of an ideal gas undergoes a process whose molar heat capacity is 4R and in which work done by gas for small change in temperature is given by the relation dW=2RdT, then the ratio CPCV is
7/5
5/3
3/2
2
The correct Answer is:C
To solve the problem, we need to find the ratio CPCV for an ideal gas undergoing a specific process. We are given that the molar heat capacity C for the process is 4R and the work done by the gas for a small change in temperature is given by dW=2RdT.
1. Understand the Given Information:
- Molar heat capacity for the process: C=4R
- Work done by the gas: dW=2RdT
- Number of moles n=1 (since it is given as one mole of gas).
2. Apply the First Law of Thermodynamics:
The first law states:
dQ=dU+dW
where dQ is the heat added to the system, dU is the change in internal energy, and dW is the work done by the system.
3. Express dQ in Terms of Molar Heat Capacity:
Since we have one mole of gas, we can express dQ as:
dQ=nCdT=1⋅CdT=CdT
Substituting the value of C:
dQ=4RdT
4. Substitute dW into the First Law Equation:
Now substituting dQ and dW into the first law equation:
4RdT=dU+2RdT
5. Rearranging the Equation:
Rearranging gives:
dU=4RdT−2RdT=2RdT
6. Relate Change in Internal Energy to Heat Capacities:
The change in internal energy dU can also be expressed in terms of CV:
dU=nCVdT=1⋅CVdT=CVdT
Thus, we have:
CVdT=2RdT
This implies:
CV=2R
7. Calculate CP:
We know the relation between CP and CV for an ideal gas:
CP−CV=R
Substituting CV=2R:
CP−2R=R
Therefore:
CP=3R
8. Find the Ratio CPCV:
Now we can find the ratio:
CPCV=3R2R=32
Final Answer:
The ratio CPCV is 32.
- Molar heat capacity for the process: C=4R
- Work done by the gas: dW=2RdT
- Number of moles n=1 (since it is given as one mole of gas).
The first law states:
dQ=dU+dW
where dQ is the heat added to the system, dU is the change in internal energy, and dW is the work done by the system.
Since we have one mole of gas, we can express dQ as:
dQ=nCdT=1⋅CdT=CdT
Substituting the value of C:
dQ=4RdT
Now substituting dQ and dW into the first law equation:
4RdT=dU+2RdT
Rearranging gives:
dU=4RdT−2RdT=2RdT
The change in internal energy dU can also be expressed in terms of CV:
dU=nCVdT=1⋅CVdT=CVdT
Thus, we have:
CVdT=2RdT
This implies:
CV=2R
We know the relation between CP and CV for an ideal gas:
CP−CV=R
Substituting CV=2R:
CP−2R=R
Therefore:
CP=3R
Now we can find the ratio:
CPCV=3R2R=32
The ratio CPCV is 32.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0282videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
One mole of an ideal gas undergoes a process whose molar heat capacity is 4R and in which work done by gas for small change in temperature is given by the relation dW=2RdT, then find the degree of freedom of gas
View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View Solution
Knowledge Check
- Question 1 - Select One
An ideal gas undergoes cyclic process ABCDA as shown in given p−V diagram. The amount of work done by the gas is
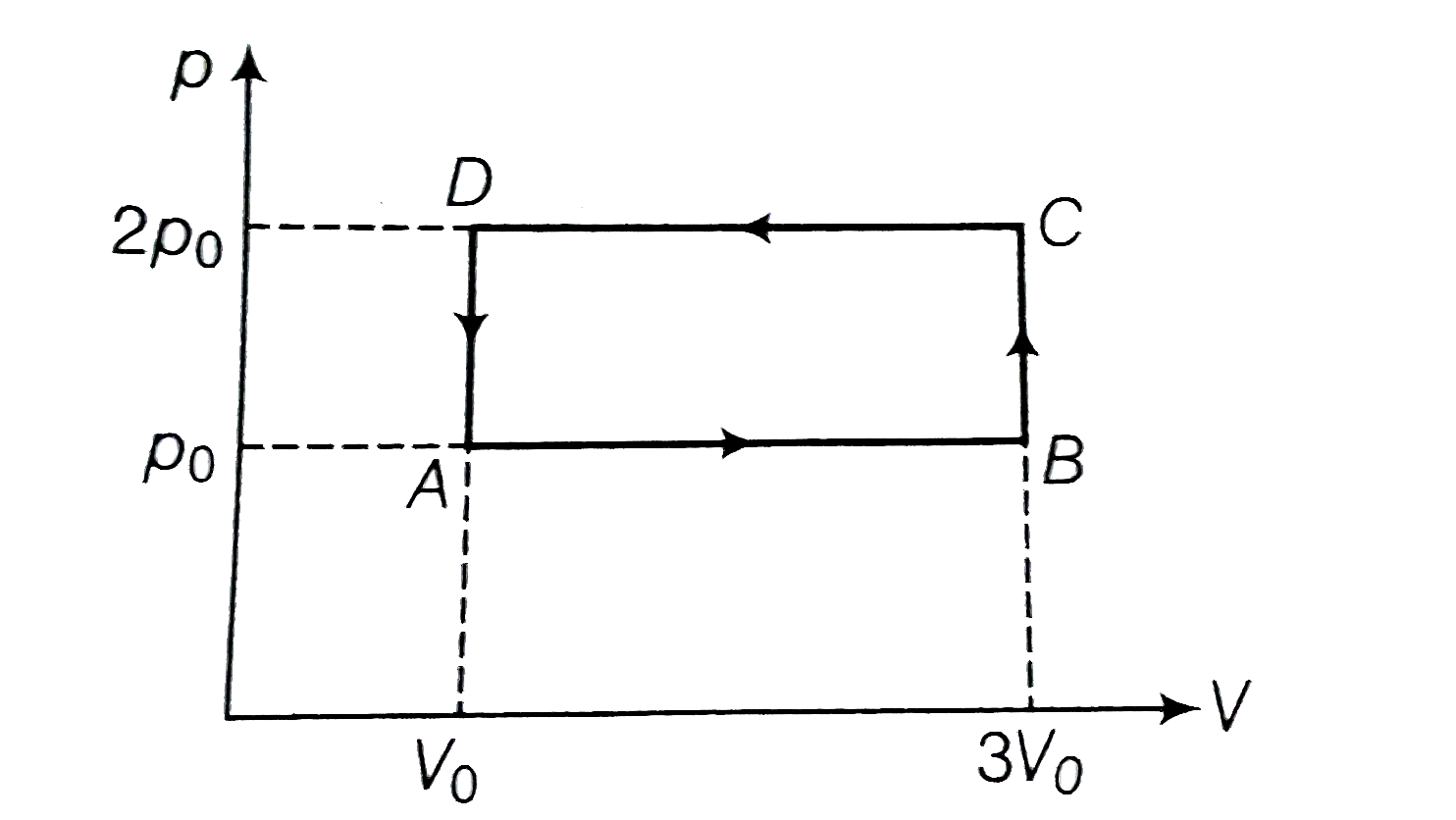 A6P0V0B−2P0V0C+2P0V0D+4P0V0
A6P0V0B−2P0V0C+2P0V0D+4P0V0
One mole of an ideal gas undergoes a process T = 300 + 2V. Then amount of work done by gas when volume increases from 2m3 to 4m3:
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
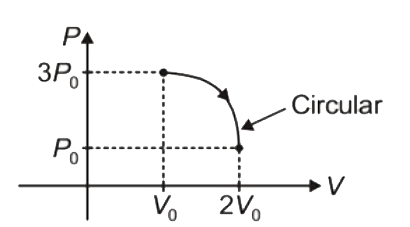 View Solution
View Solutionn moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
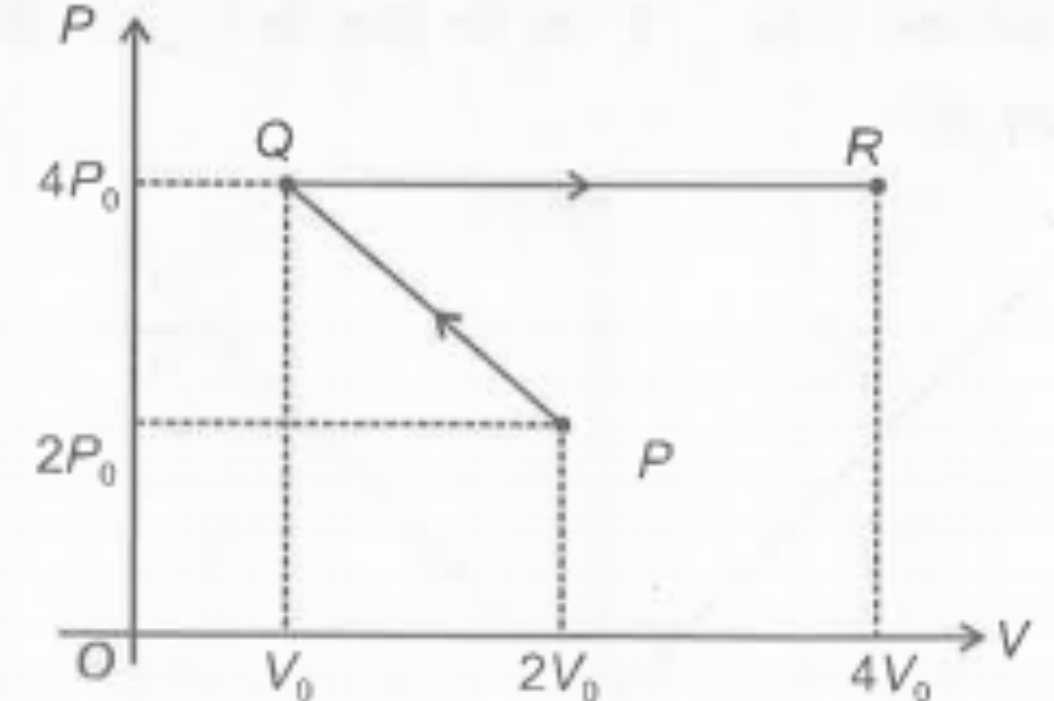 View Solution
View SolutionOne mole of an ideal monatomic gas undergoes the process p=αT1/2, where α is a constant.
(a) Find the work done by the gas if its temperature increases by 50K.
(b) Also, find the molar specific heat of the gas.View SolutionOne mole of an ideal monatomic gas undergoes the process p=αT1/2, where α is a constant.
(a) Find the work done by the gas if its temperature increases by 50K.
(b) Also, find the molar specific heat of the gas.View SolutionAn ideal gas undergoes cyclic process ABCDA as shown in givend p−V diagram. The amount of work done by the gas is
 View Solution
View Solution

