An irregular rod of same uniform material as shown in figure is conducting heat at a steady rate. The temperature gradient at various sections versus area of cross section graph will be
_S01_094_Q01.png)
_S01_094_O01.png)
_S01_094_O02.png)
_S01_094_O03.png)
_S01_094_O04.png)
The correct Answer is:B
H=KAdTdx is same in steady condition, ∴AdTdx = constant ∴ rectangular hyperbolic graph
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0282videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
Find the temperature of junction at B, if each rod has equal area of cross-section.
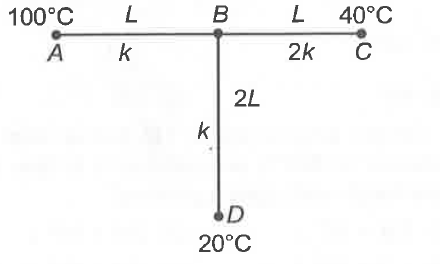View SolutionA rod is heated at one end as shown in figure. In steady state temperature of different sections becomes constant but not same. Why so?
. View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
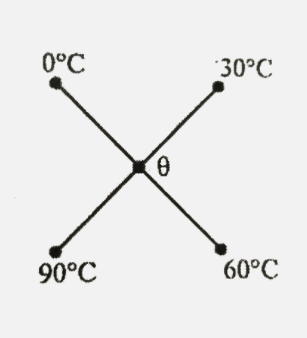View SolutionTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
View SolutionThe two ends of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. The temperature gradientat any point on the rod is dθdl(equal to the difference in temperature per unit length). The heat flow per unit time per unit cross-section of the rod is l then which of the following statements is/are correct:
View SolutionA metal rod of cross sectional area 1.0cm2 is being heated at one end. At one time , the temperature gradient is 5.0∘Ccm−1 at cross section A and is 2.5∘Ccm−1 at cross section B. calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB=0.40J∘C−1 , thermal conductivity of the material of the rod. K=200Wm−1C−1 . Neglect any loss of heat to the atmosphere.
View Solutionon heating a cylindrical metallic rod, its length increases by 2% . Then area of cross section of rod will
View SolutionThe ends of a long bar are maintained at different temperatures and there is no loss of heat from the sides of the bar due to conduction or radiation. The graph of temperature against distance of the bar when it has attained steady state is shown here. The graph shows (i) the temperature gradient is not uniform.
(ii) the bar has uniform cross-sectional area.
(iii) the cross-sectional area of the bar increases as the distance from the hot end increases.
(iv) the cross-sectional area of the bar becreases as the distance from the hot end increasesView SolutionTwo different rods A and B are kept as shown in figure . The variation of temperature of different cross sections with distance is plotted in a graph shown in figure . The ration of thermal conductivities of A andB is -
_E01_027_Q01.png)
View SolutionConside the situation shown in figure. The frame is made of the same material and has a unifrom cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100∘C is 130J .
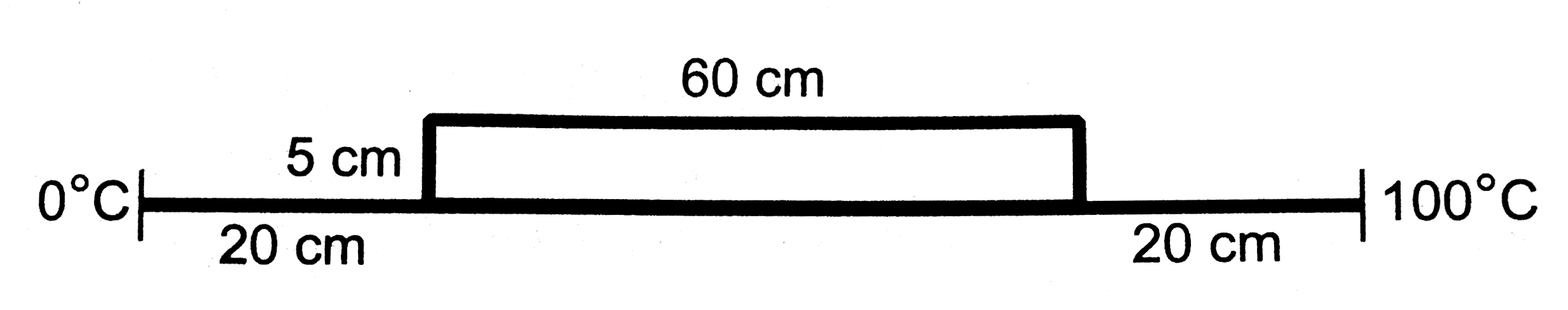View Solution