In a 10 m deep lake, the bottom is at a constant temperature of 4∘C. The air temperature is constant at −4∘C.Kice=3Kω. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
7.5m
6m
5 m
2.5m
The correct Answer is:A
To solve the problem, we need to determine the maximum thickness of ice that can form on a 10 m deep lake, given the temperature conditions and the thermal conductivity of ice and water. Let's break down the solution step by step.
1. Understanding the Setup:
- The lake is 10 m deep.
- The bottom of the lake is at a constant temperature of 4∘C.
- The air temperature is at −4∘C.
- The thermal conductivity of ice (Kice) is 3 times that of water (Kwater).
2. Defining Variables:
- Let X be the thickness of the ice.
- The depth of water below the ice will be 10−X.
3. Setting Up Heat Flow Equations:
- The heat flow through the ice layer can be expressed as:
I=4−0Rice(from the air at -4°C to the ice at 0°C)
- The heat flow through the water layer can be expressed as:
I=0−4Rwater(from the water at 4°C to the ice at 0°C)
4. Expressing Thermal Resistances:
- The thermal resistance for the ice layer is:
Rice=XKice⋅A=X3Kwater⋅A
- The thermal resistance for the water layer is:
Rwater=10−XKwater⋅A
5. Equating Heat Flows:
- Since the heat flows are equal, we can set the two equations equal to each other:
4Rice=4Rwater
- Substituting the expressions for Rice and Rwater:
4X3Kwater⋅A=410−XKwater⋅A
- Simplifying this gives:
4⋅3Kwater⋅AX=4⋅Kwater⋅A10−X
6. Canceling Common Terms:
- Cancel 4, Kwater, and A from both sides:
3X=110−X
7. Cross-Multiplying:
- Cross-multiplying gives:
3(10−X)=X
- Expanding this results in:
30−3X=X
8. Solving for X:
- Rearranging the equation:
30=4X
- Therefore:
X=304=7.5 m
Conclusion:
The maximum thickness of ice that can form on the lake is 7.5 meters.
- The lake is 10 m deep.
- The bottom of the lake is at a constant temperature of 4∘C.
- The air temperature is at −4∘C.
- The thermal conductivity of ice (Kice) is 3 times that of water (Kwater).
- Let X be the thickness of the ice.
- The depth of water below the ice will be 10−X.
- The heat flow through the ice layer can be expressed as:
I=4−0Rice(from the air at -4°C to the ice at 0°C)
- The heat flow through the water layer can be expressed as:
I=0−4Rwater(from the water at 4°C to the ice at 0°C)
- The thermal resistance for the ice layer is:
Rice=XKice⋅A=X3Kwater⋅A
- The thermal resistance for the water layer is:
Rwater=10−XKwater⋅A
- Since the heat flows are equal, we can set the two equations equal to each other:
4Rice=4Rwater
- Substituting the expressions for Rice and Rwater:
4X3Kwater⋅A=410−XKwater⋅A
- Simplifying this gives:
4⋅3Kwater⋅AX=4⋅Kwater⋅A10−X
- Cancel 4, Kwater, and A from both sides:
3X=110−X
- Cross-multiplying gives:
3(10−X)=X
- Expanding this results in:
30−3X=X
- Rearranging the equation:
30=4X
- Therefore:
X=304=7.5 m
The maximum thickness of ice that can form on the lake is 7.5 meters.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0310videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON36videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
In an 20 m deep lake, the bottom is at a constant temperature of 4∘C. The air temperature is constant at −10∘C. The thermal conductivity of ice in 4 times that water. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
View SolutionOne kg of ice at 0∘C is mixed with 1 kg of water at 10∘C. The resulting temperature will be
View SolutionA : At higher temperature , Kw of water remains unaltered.
R: kw is a constant.View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
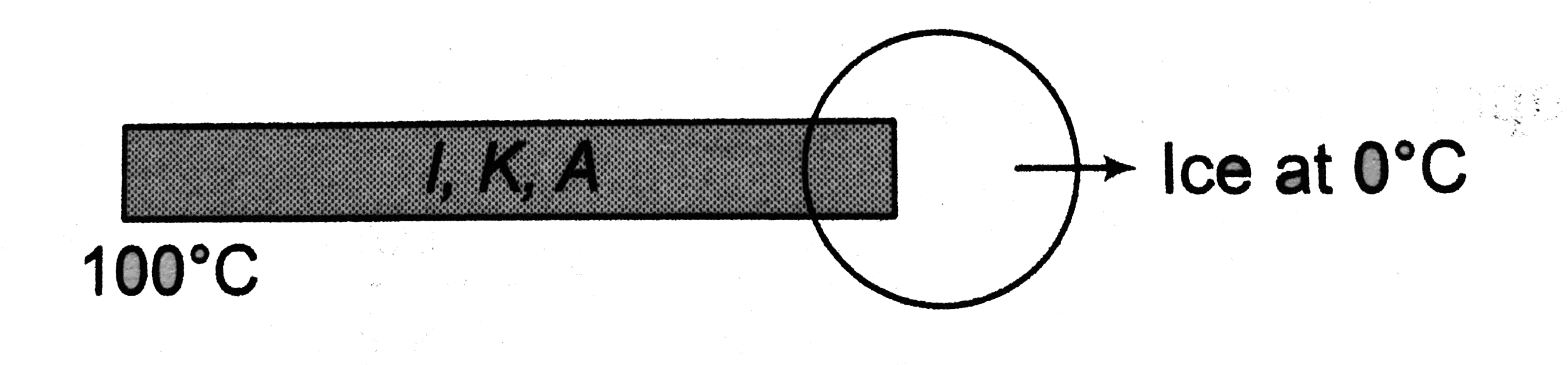 . View Solution
. View Solution1kg ice at −10∘ is mixed with 1kg water at 50∘C. The final equilibrium temperature and mixture content.
View SolutionMost substances contract on freezing . However, water does not belong to this category. We know that water expands on freezing. Further , coefficient of volume expansion of water in the temperature range from 0∘C to 4∘C is negative and above 4∘C it is positive . This behaviour of water shapes the freezing of lakes as the atmospheric temperature goes down and it is still above 4∘C.
If the atmospheric temperature is below 0∘C and ice begins to form at t = 0 , thickness of ice sheet formed up to a time 't' will be directly proprotional toView SolutionThe temperature of water at the surface of a deep lake is 2∘C. The temperature expected at the bottom is
View SolutionAn air bubble of 20cm3 volume is at the bottom of a lake 40m deep where the temperature is 4∘C. The bubble rises to the surface which is at a temperature of 20∘C. Take the temperature to be the same as that of the surrounding water and find its volume just before it reaches the surface.
View SolutionBottom of a lake is at 0∘C and atmospheric temperature is −20∘C. If 1 cm ice is formed on the surface in 24 h, then time taken to form next 1 cm of ice is
View SolutionAt a certain temperature , Kw of water is 9.0×10−14 . The pH of water at this temperature is
View Solution

