In an 20 m deep lake, the bottom is at a constant temperature of 4∘C. The air temperature is constant at −10∘C. The thermal conductivity of ice in 4 times that water. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
2211 m
20011 m
20m
10 m
The correct Answer is:B
To solve the problem of determining the maximum thickness of ice that can form on a lake with a given temperature profile, we can follow these steps:
1. Understanding the Setup:
- The lake is 20 m deep.
- The bottom temperature is constant at 4°C.
- The air temperature is -10°C.
- The thermal conductivity of ice is 4 times that of water.
2. Defining Variables:
- Let x be the thickness of the ice.
- The thickness of the water below the ice is 20−x.
3. Heat Flow Concept:
- At steady state, the heat flow through the ice must equal the heat flow through the water.
- The heat flow rate can be expressed using Fourier's law of heat conduction:
dQdt=kAΔTΔx
- Here, k is the thermal conductivity, A is the cross-sectional area, ΔT is the temperature difference, and Δx is the thickness.
4. Setting Up the Heat Flow Equations:
- For the ice:
dQdt=4kA(0−(−10))x=4kA10x
- For the water:
dQdt=kA(4−0)(20−x)=kA420−x
5. Equating the Heat Flows:
- Since the heat flow through the ice equals the heat flow through the water at steady state:
4kA10x=kA420−x
6. Canceling Common Terms:
- We can cancel kA from both sides:
4⋅10⋅(20−x)=4x
7. Simplifying the Equation:
- This simplifies to:
40(20−x)=4x
- Expanding gives:
800−40x=4x
- Rearranging results in:
800=44x
8. Solving for x:
- Dividing both sides by 44:
x=80044=20011≈18.18 m
9. Conclusion:
- The maximum thickness of ice that can form on the lake is approximately 20011 m.
- The lake is 20 m deep.
- The bottom temperature is constant at 4°C.
- The air temperature is -10°C.
- The thermal conductivity of ice is 4 times that of water.
- Let x be the thickness of the ice.
- The thickness of the water below the ice is 20−x.
- At steady state, the heat flow through the ice must equal the heat flow through the water.
- The heat flow rate can be expressed using Fourier's law of heat conduction:
dQdt=kAΔTΔx
- Here, k is the thermal conductivity, A is the cross-sectional area, ΔT is the temperature difference, and Δx is the thickness.
- For the ice:
dQdt=4kA(0−(−10))x=4kA10x
- For the water:
dQdt=kA(4−0)(20−x)=kA420−x
- Since the heat flow through the ice equals the heat flow through the water at steady state:
4kA10x=kA420−x
- We can cancel kA from both sides:
4⋅10⋅(20−x)=4x
- This simplifies to:
40(20−x)=4x
- Expanding gives:
800−40x=4x
- Rearranging results in:
800=44x
- Dividing both sides by 44:
x=80044=20011≈18.18 m
- The maximum thickness of ice that can form on the lake is approximately 20011 m.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
In a 10 m deep lake, the bottom is at a constant temperature of 4∘C. The air temperature is constant at −4∘C.Kice=3Kω. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
View SolutionIf the depth of a lake is 10 m, and the temperature of surroundings is −10∘C and that of water at the bottom of the lake is 5∘C. The thermal conductivity of the Ice and water are Kf and Kw respectively. The depth of ice will be
View Solution
Knowledge Check
What is the resulting temperature when 150 g of ice at 0∘C mixed with 300 g of water at 50∘C ?
A25∘CB33.3∘CC13.4∘CD6.6∘C
The temperature of water at the surface of a deep lake is 2∘C. The temperature expected at the bottom is
View SolutionIce has formed on a shallow pond, and a steady state has been reached, with the air above the ice at −5.0∘C and the bottom of the pond at 40∘C. If the total depth of ice + water is 1.4m, (Assume that the thermal conductivities of ice and water are 0.40 and 0.12cal/mC∘s, respectively.)
The thickness of ice layer is
View Solution10 grams of ice at −20∘C is added to 10 grams of water at 50∘C. The amount of ice and water that are present at equilibrium respectively
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
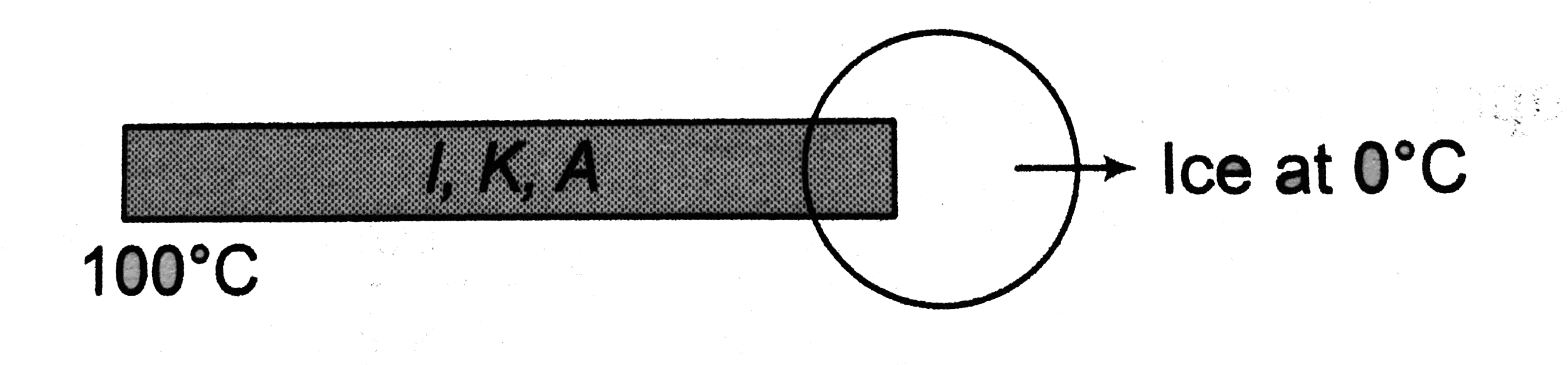 .
.
View SolutionA layer of ice of thickness y is on the surface of a lake. The air is at a constant temperature −θ∘C and the ice water interface is at 0∘C. Show that the rate at which the thickness increases is given by
dydt=KθLρy
where, K is the thermal conductivity of the ice, L the latent heat of fusion and ρ is the density of the ice.
View SolutionOn a winter day when the atmospheric temperature drops to −10∘C , ice forms on the surface of a lake. (a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed. (b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches 0∘C before the ice starts forming. Density of water =1000kgm−3 , latent heat of fusion of ice =3.36×105Jkg−1 and thermal conductivity of ice =1.7Wm−1C−1 . Neglect the expansion of water on freezing.
View SolutionIce at −20∘C mixed with 200g water at 25∘C. If temperature of mixture is 10∘C then mass of ice is -
View Solution
