A man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road and a=2×10−6/m. What is the actual length of the road, man is able to see
2000m
390m
infinite distance
None of these
The correct Answer is:A
To solve the problem step by step, we need to determine the actual length of the road that the man can see, taking into account the variation of the refractive index with height.
Step 1: Understand the given parameters
- Height of the man (H) = 2 m
- Variation of refractive index with height (y):
μ=μ0√1+ay
where a=2×10−6m−1.
Step 2: Set up the relationship between the angles and the refractive indices
Using Snell's law, we have:
μsinθ=μ0sin90∘
Since sin90∘=1, this simplifies to:
μsinθ=μ0
Thus, we can express sinθ as:
sinθ=μ0μ=1√1+ay
Step 3: Relate the angles to the distance
Using the small angle approximation, we can relate the differential distances:
dxdy=tanθ≈sinθ
This gives us:
dx=dy√1+ay
Step 4: Integrate to find the total distance
To find the total distance x that the man can see, we integrate from y=0 to y=2 (the height of the man):
x=∫20dy√1+ay
Step 5: Solve the integral
Substituting a=2×10−6:
x=∫20dy√1+2×10−6y
This integral can be solved using a substitution method. Let:
u=1+2×10−6y⟹du=2×10−6dy⟹dy=du2×10−6
When y=0, u=1 and when y=2, u=1+4×10−6.
Thus, the integral becomes:
x=∫1+4×10−611√u⋅du2×10−6=12×10−6(2√u)1+4×10−61
Calculating this gives:
x=12×10−6(2√1+4×10−6−2)
Using the approximation √1+x≈1+x2 for small x:
√1+4×10−6≈1+2×10−6
Thus:
x≈12×10−6(2(1+2×10−6)−2)=12×10−6⋅4×10−6=2m
Step 6: Final calculation
The total distance x that the man can see is approximately:
x=2000m=2km
Conclusion
The actual length of the road that the man is able to see is 2000 meters or 2 kilometers.
---
- Height of the man (H) = 2 m
- Variation of refractive index with height (y):
μ=μ0√1+ay
where a=2×10−6m−1.
Using Snell's law, we have:
μsinθ=μ0sin90∘
Since sin90∘=1, this simplifies to:
μsinθ=μ0
Thus, we can express sinθ as:
sinθ=μ0μ=1√1+ay
Using the small angle approximation, we can relate the differential distances:
dxdy=tanθ≈sinθ
This gives us:
dx=dy√1+ay
To find the total distance x that the man can see, we integrate from y=0 to y=2 (the height of the man):
x=∫20dy√1+ay
Substituting a=2×10−6:
x=∫20dy√1+2×10−6y
u=1+2×10−6y⟹du=2×10−6dy⟹dy=du2×10−6
When y=0, u=1 and when y=2, u=1+4×10−6.
x=∫1+4×10−611√u⋅du2×10−6=12×10−6(2√u)1+4×10−61
Calculating this gives:
x=12×10−6(2√1+4×10−6−2)
Using the approximation √1+x≈1+x2 for small x:
√1+4×10−6≈1+2×10−6
Thus:
x≈12×10−6(2(1+2×10−6)−2)=12×10−6⋅4×10−6=2m
The total distance x that the man can see is approximately:
x=2000m=2km
The actual length of the road that the man is able to see is 2000 meters or 2 kilometers.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0282videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road a =1.5×10−6/m. What is the apparent length of the road man is able to sec?
View SolutionA man of height 2.0m is standing on a level road because of temprature variation the refractive index of air is varying as μ=√1+ay, where y is height from road. If a=2.0×10−6m−1. Then, find distant point that he can see on the road.
View SolutionDue to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as n=n0√1+ay, where n0 is the index of refraction at the surface and a=2.0×10−6m−1 . A person of height h=2.0m stands on a level surface. Beyond what distance will he not see the runway?
 View Solution
View SolutionA long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr) where μ1 and r(>d) are constants. The refractive index of air is μ0
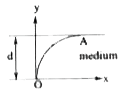
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary isView SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
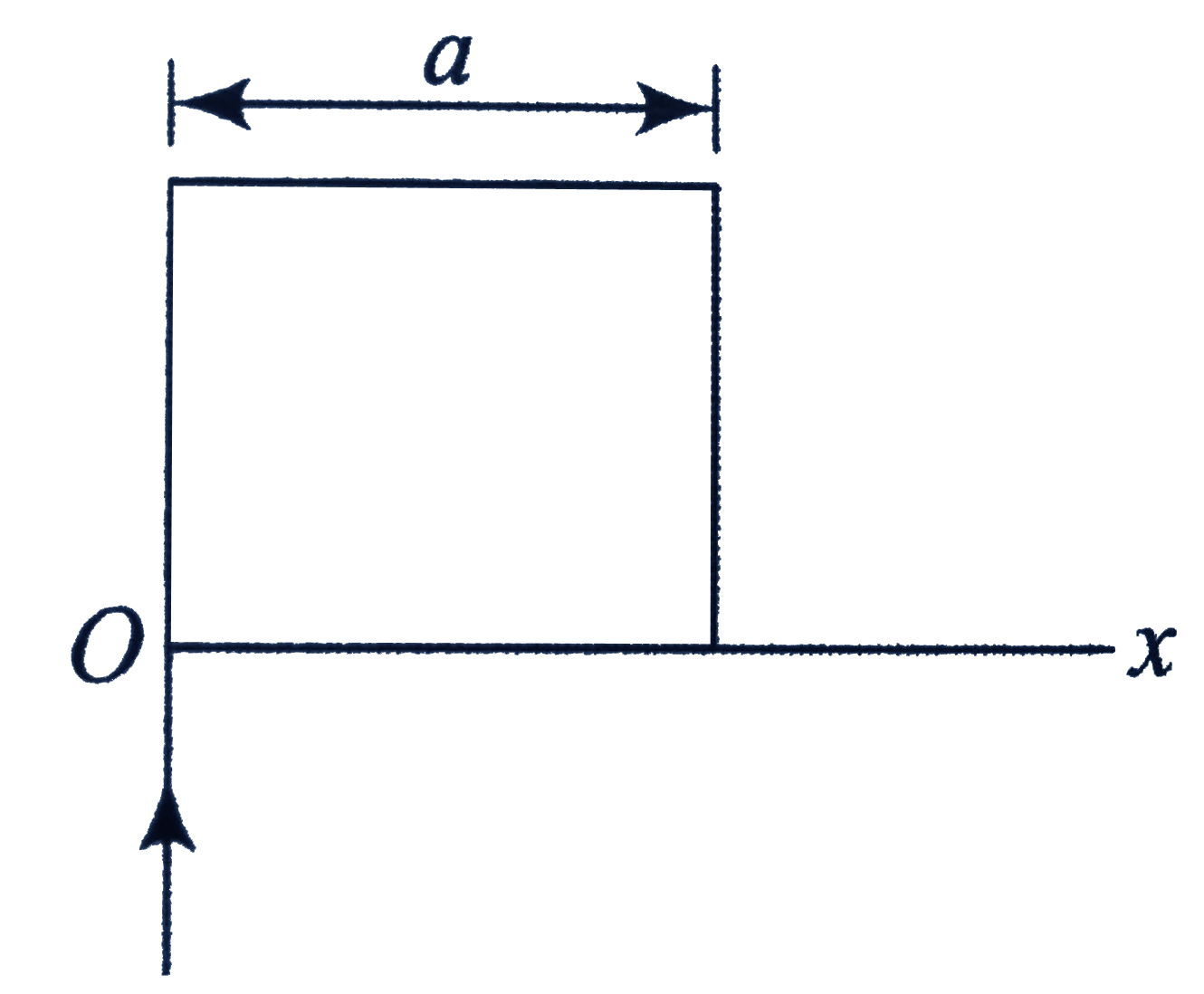 View Solution
View SolutionA ray hits the y-axis making an angle θ with y-axis as shown in the figure. The variation of refractive index with x-coordinate is μ=μ0(1−xd) for 0≤x≤d(1−1μ0) and μ=μ0 for x<0, where d is a positive constant. The maximum x-coordinate of the path traced by the ray is
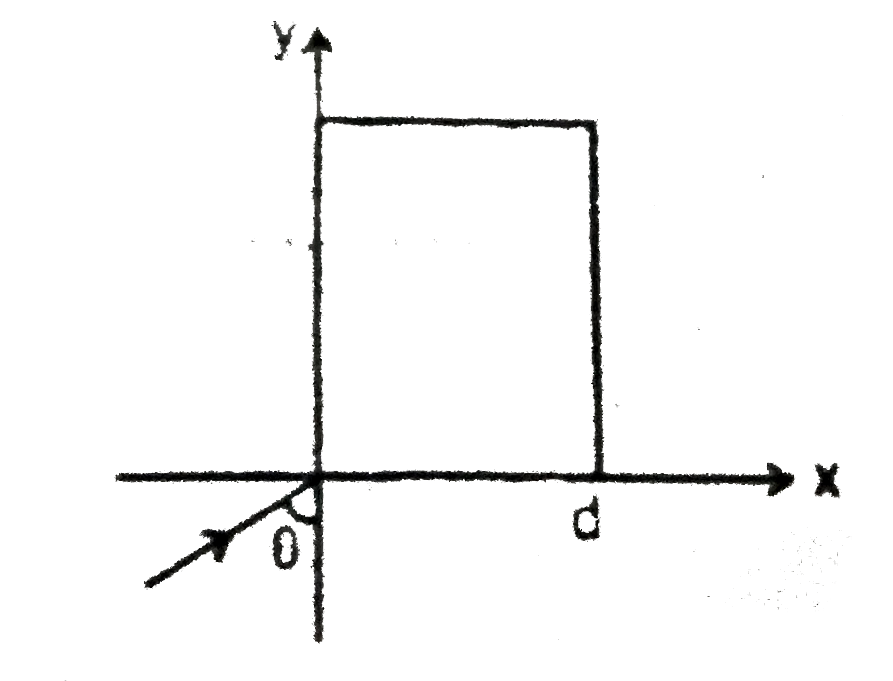 View Solution
View SolutionThe figure shows a transparent slab of length m placed in air whose refractive index in x direction varies as μ=1+x2(0<x<1). The optical path length of ray R will be
 View Solution
View SolutionThe refractive index of diamond is 2.42, whereas for air it is 1.0. What does it tell you about optical density and speed of light in air and in diamond?
View SolutionA light of wavelength 6000Å shines on two narrow slits separeted by a distance 1.0 mm and illuminates a screen at a distance 1.5 m away. When one slit is covered by a thin glass plate of refractive index 1.8 and other slit by a thin glass plate of refractive index μ, the central maxima shifts by 0.1 rad. Both plates have the same thickness of 0.5 mm. The value of refractive index μ of the glass is
View SolutionAn object O is placed in front of a convex lens such that the lens forms a sharp image on the screen. The distance between the object and screen is 10 cm. The lens is made of glass at refractive index μg=32. The surrounding medium is air with refractive index 1.
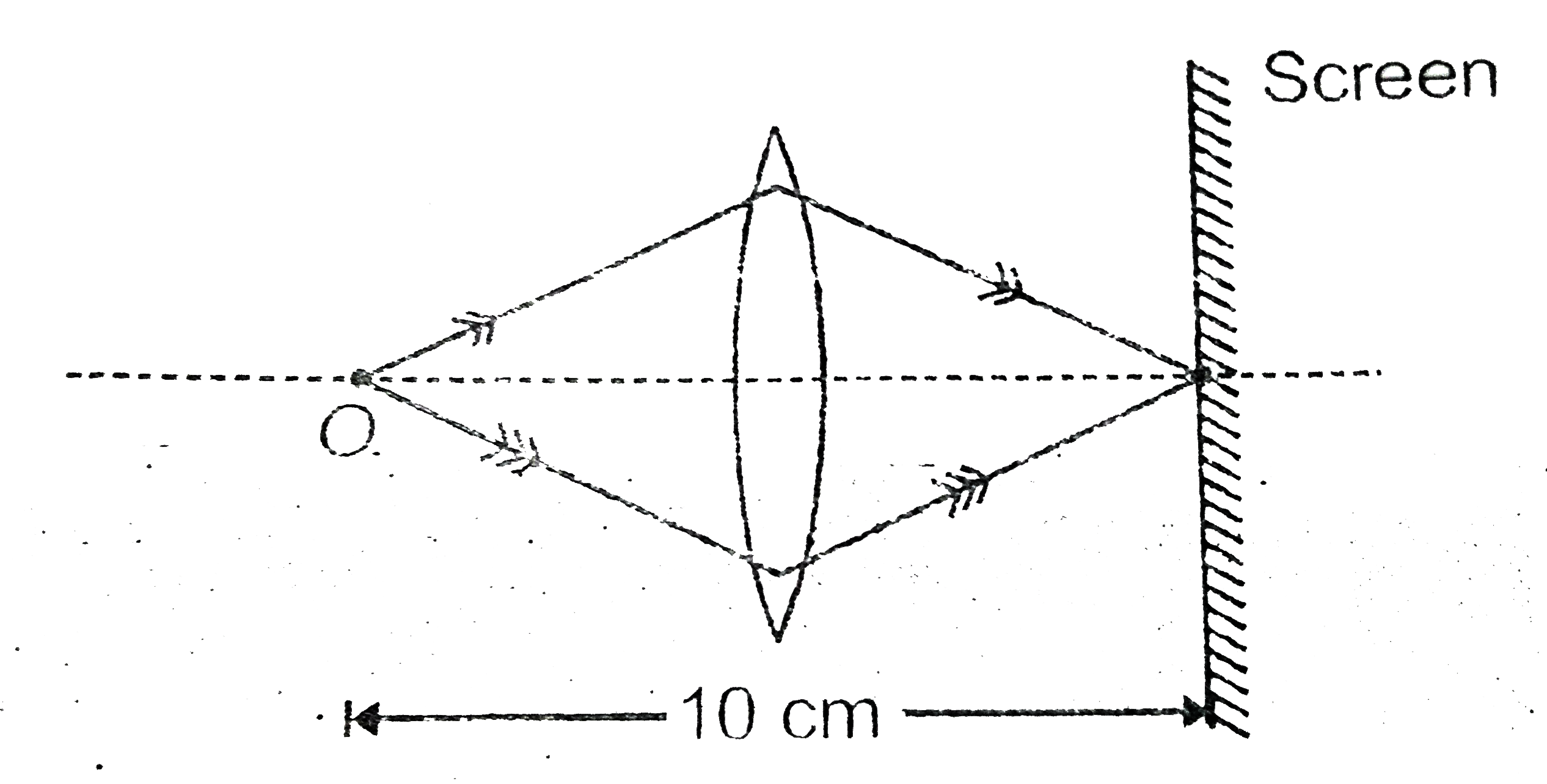
The focal length of the lens, used in the above experiment, satisfies the condition given byView Solution

