The velocity of a particle in S.H.M. at positions x1 and x2 are v1 and v2 respectively. Determine value of time period and amplitude.
To solve the problem, we need to determine the time period (T) and amplitude (A) of a particle in Simple Harmonic Motion (SHM) given its velocities (v1 and v2) at two different positions (x1 and x2).
1. Understanding the Velocity in SHM:
The velocity (v) of a particle in SHM can be expressed as:
v=ω√A2−x2
where ω is the angular frequency, A is the amplitude, and x is the position of the particle.
2. Setting Up Equations:
For position x1 with velocity v1:
v1=ω√A2−x21(Equation 1)
For position x2 with velocity v2:
v2=ω√A2−x22(Equation 2)
3. Squaring Both Equations:
Squaring both equations gives:
v21=ω2(A2−x21)(1)
v22=ω2(A2−x22)(2)
4. Subtracting the Two Equations:
Subtract Equation (2) from Equation (1):
v21−v22=ω2(A2−x21)−ω2(A2−x22)
This simplifies to:
v21−v22=ω2(x22−x21)
5. Solving for Angular Frequency (ω):
Rearranging gives:
ω2=v21−v22x22−x21
Therefore,
ω=
⎷v21−v22x22−x21
6. Finding the Time Period (T):
The time period T is related to angular frequency by:
T=2πω
Substituting ω gives:
T=2π√v21−v22x22−x21
7. Finding the Amplitude (A):
To find the amplitude, we can use either of the original equations. Using Equation (1):
v21=ω2(A2−x21)
Rearranging gives:
A2=v21ω2+x21
Substituting ω2:
A2=v21(x22−x21)v21−v22+x21
Final Answers:
- Time Period T:
T=2π√v21−v22x22−x21
- Amplitude A:
A=
⎷v21(x22−x21)v21−v22+x21
The velocity (v) of a particle in SHM can be expressed as:
v=ω√A2−x2
where ω is the angular frequency, A is the amplitude, and x is the position of the particle.
For position x1 with velocity v1:
v1=ω√A2−x21(Equation 1)
For position x2 with velocity v2:
v2=ω√A2−x22(Equation 2)
Squaring both equations gives:
v21=ω2(A2−x21)(1)
v22=ω2(A2−x22)(2)
Subtract Equation (2) from Equation (1):
v21−v22=ω2(A2−x21)−ω2(A2−x22)
This simplifies to:
v21−v22=ω2(x22−x21)
Rearranging gives:
ω2=v21−v22x22−x21
Therefore,
ω=
⎷v21−v22x22−x21
The time period T is related to angular frequency by:
T=2πω
Substituting ω gives:
T=2π√v21−v22x22−x21
To find the amplitude, we can use either of the original equations. Using Equation (1):
v21=ω2(A2−x21)
Rearranging gives:
A2=v21ω2+x21
Substituting ω2:
A2=v21(x22−x21)v21−v22+x21
- Time Period T:
T=2π√v21−v22x22−x21
- Amplitude A:
A=
⎷v21(x22−x21)v21−v22+x21
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES
29 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View SolutionA particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionThe area of hole (1) is A1 and of hole (2) is A2. The velocity of efflux and range of liquid is v1,v2andx1,x2 for holes (1) and (2) respectively. The time taken by liquid, jet to reach the ground from holes (1) and (2) are t1andt2 respectively. Cross section of tank is very very large compared to size of holes.
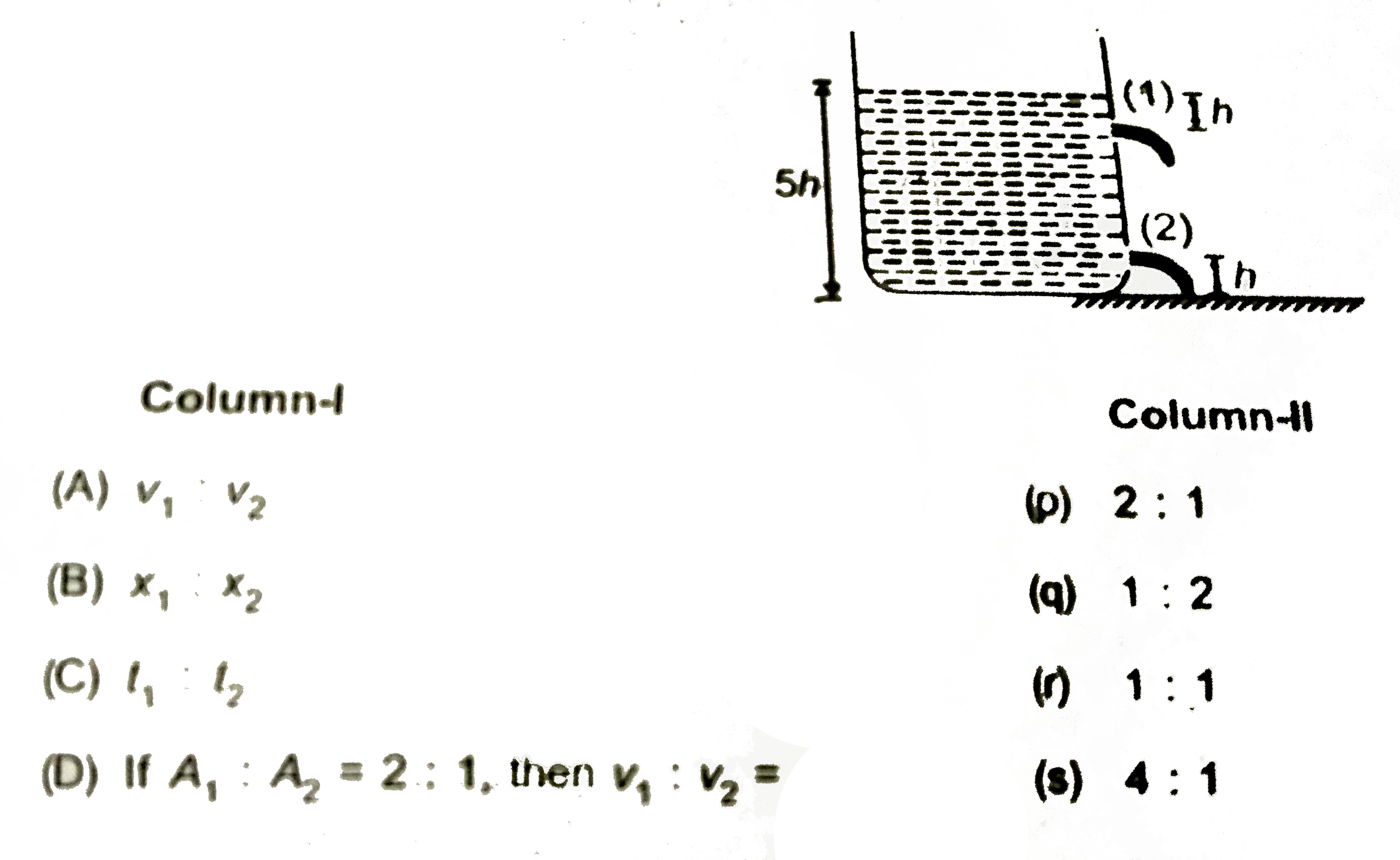
Column-IColumn-II(A)v1:v2(p)2:1(B)x1:x2(q)1:2(C)t1:t2(r)1:1(D)ifA1:A2=2:1,thenv1:v2=(s)4:1
View SolutionAssertion : The average velocity of a particle having initial and final velocity v1 and v2 is v1+v2/2.
Reason : If r1 and r2 be the initial and final displacement in time t, then vav=r1−r2t .
View SolutionTwo bodies of masses (m1) and (m2) are droppded from heithts h1 and h2, respectively. They reach the ground after time t1 and t2 and strike the ground with v1 and v2, respectively Choose the correct relations from the following.
View SolutionA particle is moving with shm in a straight line. When the distance of the particle from the equilibrium position has the value x1andx2 the corresponding values of velocities are v1andv2 show that period is T=2π[x22−x21v21−v22]1/2
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View Solution
