A solid uniform cylinder of mass M performs small oscillations in horizontal plane if slightly displaced from its mean position shown in figure. If it is given that initially springs are in natural lengths and cylinder does not slip on ground during oscillaitons due to frications between ground and cylinder. Force constant of each spring is k.
Find time period of these oscillation.
_S01_027_Q01.png)
In the sitution given in problem, the cylinder is in its equilibrium position, when position when springs are unstrained. When it slightly rolled and released, it starts excuting SHM and due to friction, the cylinder is in rollting motion. Now during oscillations we consider the cylinder when it is at a distance x from the mean position and moving with a speed v as shown in figure. As cylinder in pure rolling, its angular speed of rotation can be given as
_S01_027_S01.png)
As centre of cylinder is at a distance x from the initial position, the springs which are connected at a point on the oscillating system can be given as
ET=12mv2+12(12MR2)ω2+12k(2x)2×2
Differentiating with respect to time, we get
dETdt=12M(2vdvdt)+12(12MR2)1R2(2vdvdt)+4k(2xdxdt)=0
⇒Mva+12Mva+8kxv=0⇒a=−163kMx
Comparing equation with basic differntial equation of SHM.
We get, the angular frequency of SHM as ω=√16k3M
Thus time period these oscillation is T=2πω=2π√3M16k=π2√3Mk
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES29videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01117videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absence of sliding.
xView SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these oscillations.
 View Solution
View SolutionA solid cylinder is attached to a horizonatal massless spring as shwn in figure.If the cyclinder rolls without slipping, the time period of oscillation of the cyclinder is
 View Solution
View SolutionA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png) View Solution
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 View Solution
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 View Solution
View SolutionA block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be
 View Solution
View Solution
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k isView SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
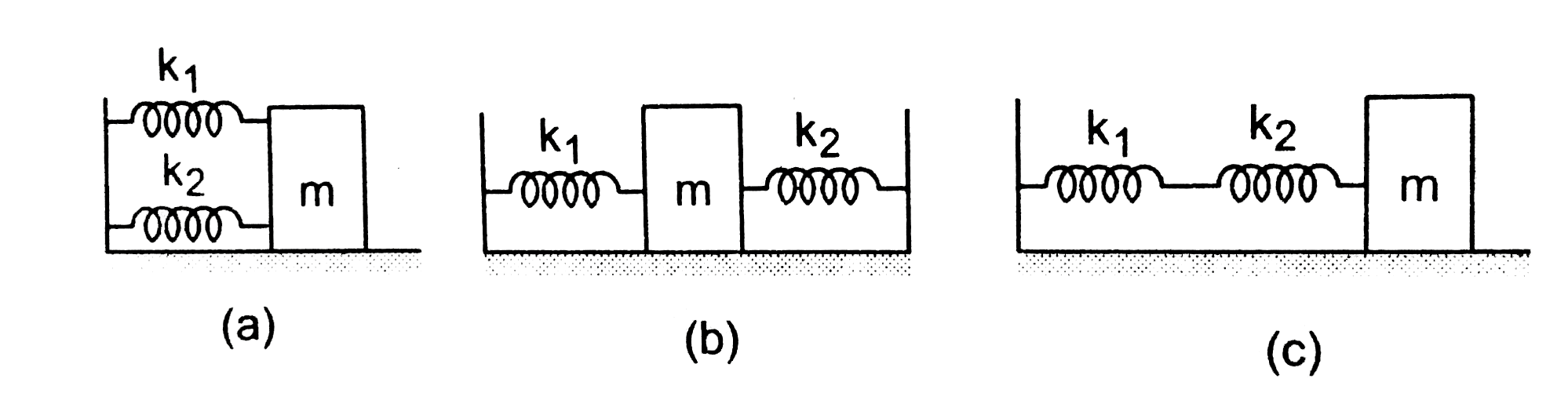 View Solution
View Solution

