A solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absence of sliding.
x
The correct Answer is:B, C
To find the period of oscillation of a solid uniform cylinder of mass m performing small oscillations due to the action of two springs with stiffness k, we can follow these steps:
Step 1: Understanding the System
The cylinder is subjected to the restoring force from two springs when it is displaced. The displacement causes a torque about the center of the cylinder.
Step 2: Define the Displacement
Let the angle of displacement of the cylinder be θ. The horizontal displacement of the ends of the springs due to this angle is 2θr, where r is the radius of the cylinder.
Step 3: Calculate the Restoring Force
The restoring force from each spring when displaced by 2θr is:
F=k⋅(2θr)
Since there are two springs, the total restoring force is:
Ftotal=2k(2θr)=4kθr
Step 4: Calculate the Torque
The torque τ due to this force about the center of the cylinder is given by:
τ=Ftotal⋅r=4kθr⋅r=4kr2θ
Step 5: Relate Torque to Angular Acceleration
Using Newton's second law for rotation, we have:
τ=Iα
where I is the moment of inertia of the cylinder about its axis and α is the angular acceleration. The moment of inertia I for a solid cylinder is:
I=12mr2
Step 6: Substitute and Rearrange
Substituting the expressions for torque and moment of inertia, we get:
4kr2θ=(12mr2)α
Since α=d2θdt2, we can rewrite this as:
4kr2θ=12mr2d2θdt2
Step 7: Simplify the Equation
Dividing both sides by r2 (assuming r≠0):
4kθ=12md2θdt2
Rearranging gives:
d2θdt2+8kmθ=0
Step 8: Identify the Angular Frequency
This is a standard form of the simple harmonic motion equation:
d2θdt2+ω2θ=0
where ω2=8km. Thus, the angular frequency ω is:
ω=√8km
Step 9: Calculate the Period
The period T of oscillation is given by:
T=2πω=2π√m8k=π4√mk
Final Answer
The period of oscillation of the cylinder is:
T=π4√mk
---
The cylinder is subjected to the restoring force from two springs when it is displaced. The displacement causes a torque about the center of the cylinder.
Let the angle of displacement of the cylinder be θ. The horizontal displacement of the ends of the springs due to this angle is 2θr, where r is the radius of the cylinder.
The restoring force from each spring when displaced by 2θr is:
F=k⋅(2θr)
Since there are two springs, the total restoring force is:
Ftotal=2k(2θr)=4kθr
The torque τ due to this force about the center of the cylinder is given by:
τ=Ftotal⋅r=4kθr⋅r=4kr2θ
Using Newton's second law for rotation, we have:
τ=Iα
where I is the moment of inertia of the cylinder about its axis and α is the angular acceleration. The moment of inertia I for a solid cylinder is:
I=12mr2
Substituting the expressions for torque and moment of inertia, we get:
4kr2θ=(12mr2)α
Since α=d2θdt2, we can rewrite this as:
4kr2θ=12mr2d2θdt2
Dividing both sides by r2 (assuming r≠0):
4kθ=12md2θdt2
Rearranging gives:
d2θdt2+8kmθ=0
This is a standard form of the simple harmonic motion equation:
d2θdt2+ω2θ=0
where ω2=8km. Thus, the angular frequency ω is:
ω=√8km
The period T of oscillation is given by:
T=2πω=2π√m8k=π4√mk
The period of oscillation of the cylinder is:
T=π4√mk
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.1
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A solid uniform cylinder of mass M performs small oscillations in horizontal plane if slightly displaced from its mean position shown in figure. If it is given that initially springs are in natural lengths and cylinder does not slip on ground during oscillaitons due to frications between ground and cylinder. Force constant of each spring is k.
Find time period of these oscillation.
_S01_027_Q01.png)
View SolutionThe time period of small oscillations of mass m :-
_S01_040_Q01.png)
View SolutionA small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.

View SolutionA uniform cylinder of mass m and radius R is in equilibrium on an inclined by the action of a light spring of stiffnesk, gravity and reaction force acting on it .If the angle of inclination of the plane is ϕ , find the angular frequency of small oscillation of the cylinder

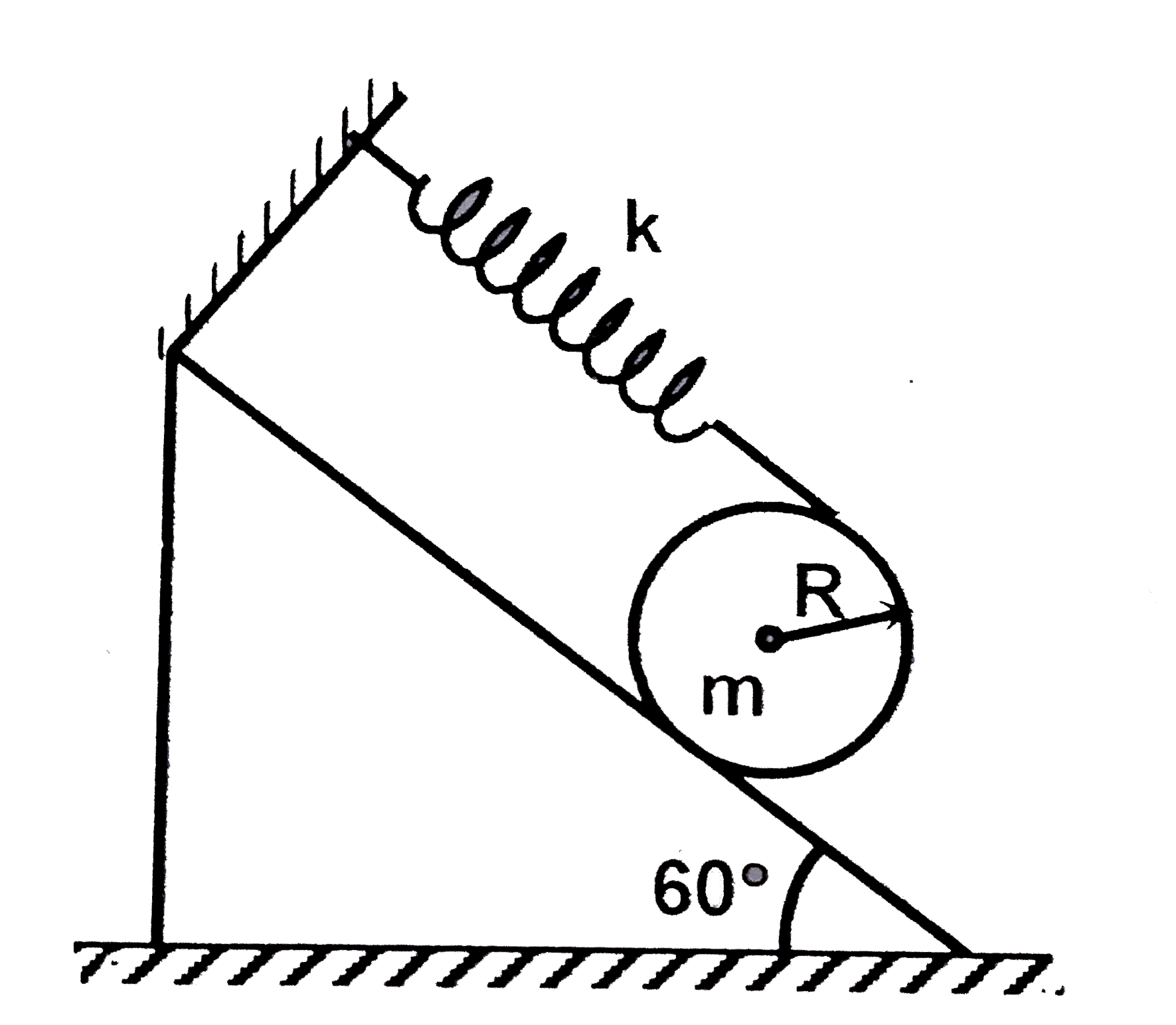
View SolutionA uniform solid sphere of mass 'm' and radius R is in equilibrium on an inclined plane by the action of the light spring of stiffness k, gravity and on it. If the angle of inclination of the plane is 60∘, then find the time period of oscillation for small displancement.
View SolutionSpring mass system is shown in figure. find the time period of vertical oscillations. The system is in vertical plane.

View Solution
A solid cylinder of mass M is attached to the spring by means of a frintionless pivot. The cylinder is placed on floor. Find the time period of small oscillation of the system, if the floor is sufficiently rought to prevent any slipping of cylinder. Assume stiffness of spring to be K.
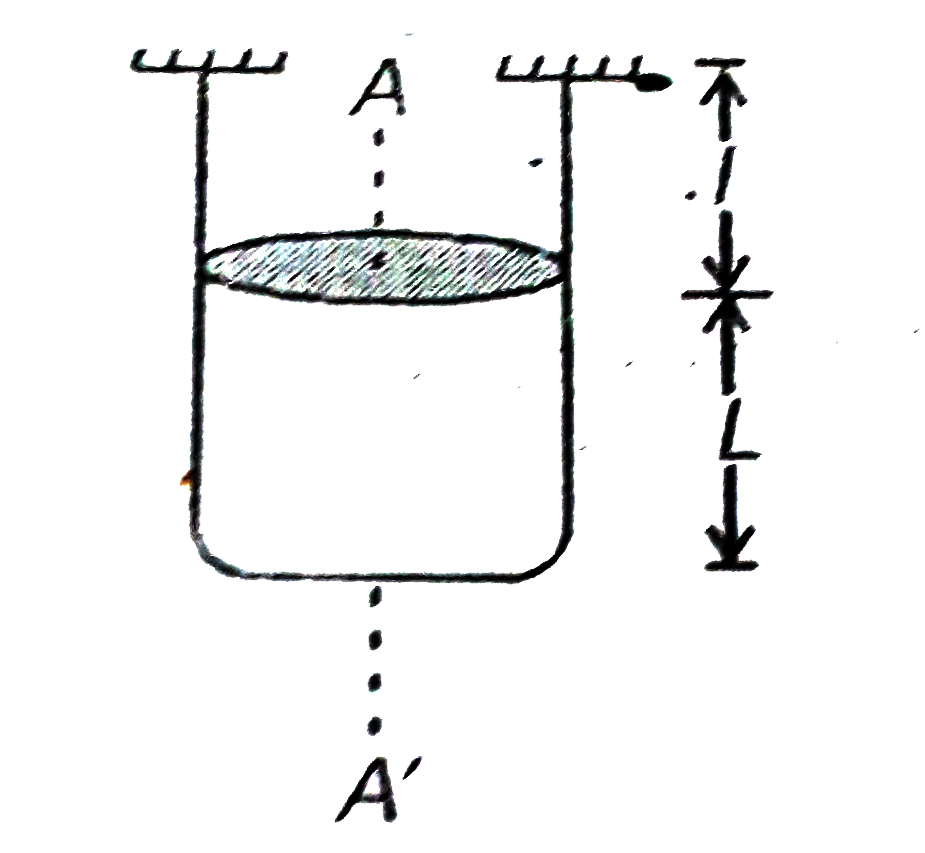
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
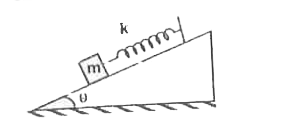
View SolutionA block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
View SolutionA disc of mass m hanged by a string is attached at P and a spring of stiffness k is attached at Q. Find the frequency of small angular oscillation of the disc if the string does not slide over the pulley. Assume l0=Ml of the dise about O.

View Solution
