A 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_052_Q01.png)
Let us now make a slight change to the initial conditions. At t=0, let the block be released from the same position with an initial velocity v1=64cm/s. Position of the block as a function of time can be expressed as
x=5sin16t
x=5sin(16t+37∘)
x=5sin(16t−37∘)
x=5cos(16t+37∘)
The correct Answer is:B
Let x=Asin(16t+ϕ)v=Aωcos(16t+ϕ) where ω2=Km=25.60.1=256⇒ω=16radsec
Att=0,3=Asinϕ & 64=Acosϕ⇒tanϕ=34⇒ϕ=37∘ Also A=5cm
Therefore equation of SHM x=5sin(16t+37∘)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:SOME WORKED OUT EXAMPLES
Explore 29 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-01
Explore 117 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
A 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_050_Q01.png)
When the block is at position A on the graph, its
View Solution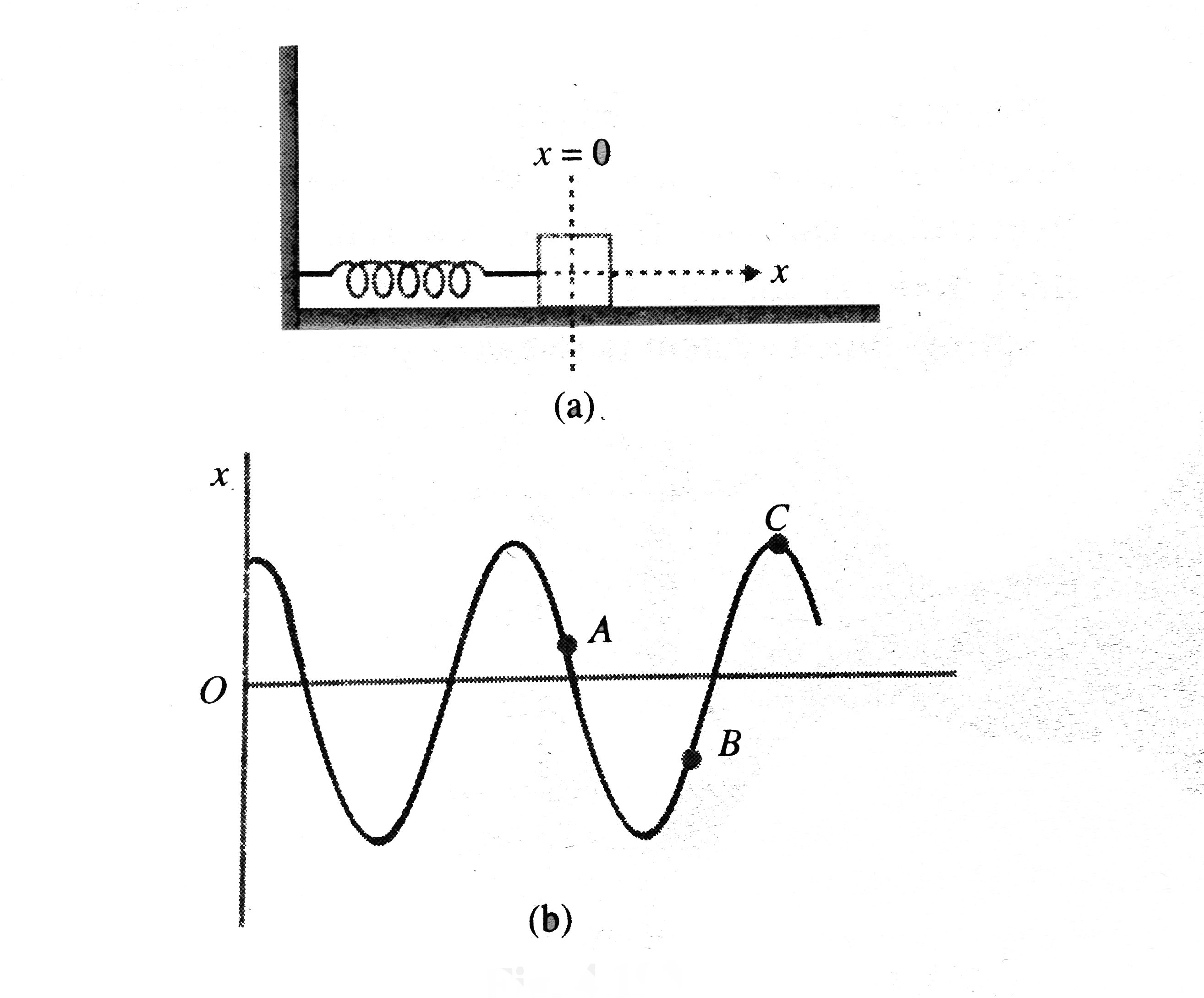
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Q. When the block is at position B on the graph its.
View Solution
Knowledge Check
A block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100N/m. the block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. the kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
A0.0375 J, 0.125 JB0.125 J, 0.375 JC0.125 J, 0.125 JD0.375 J, 0.375 J
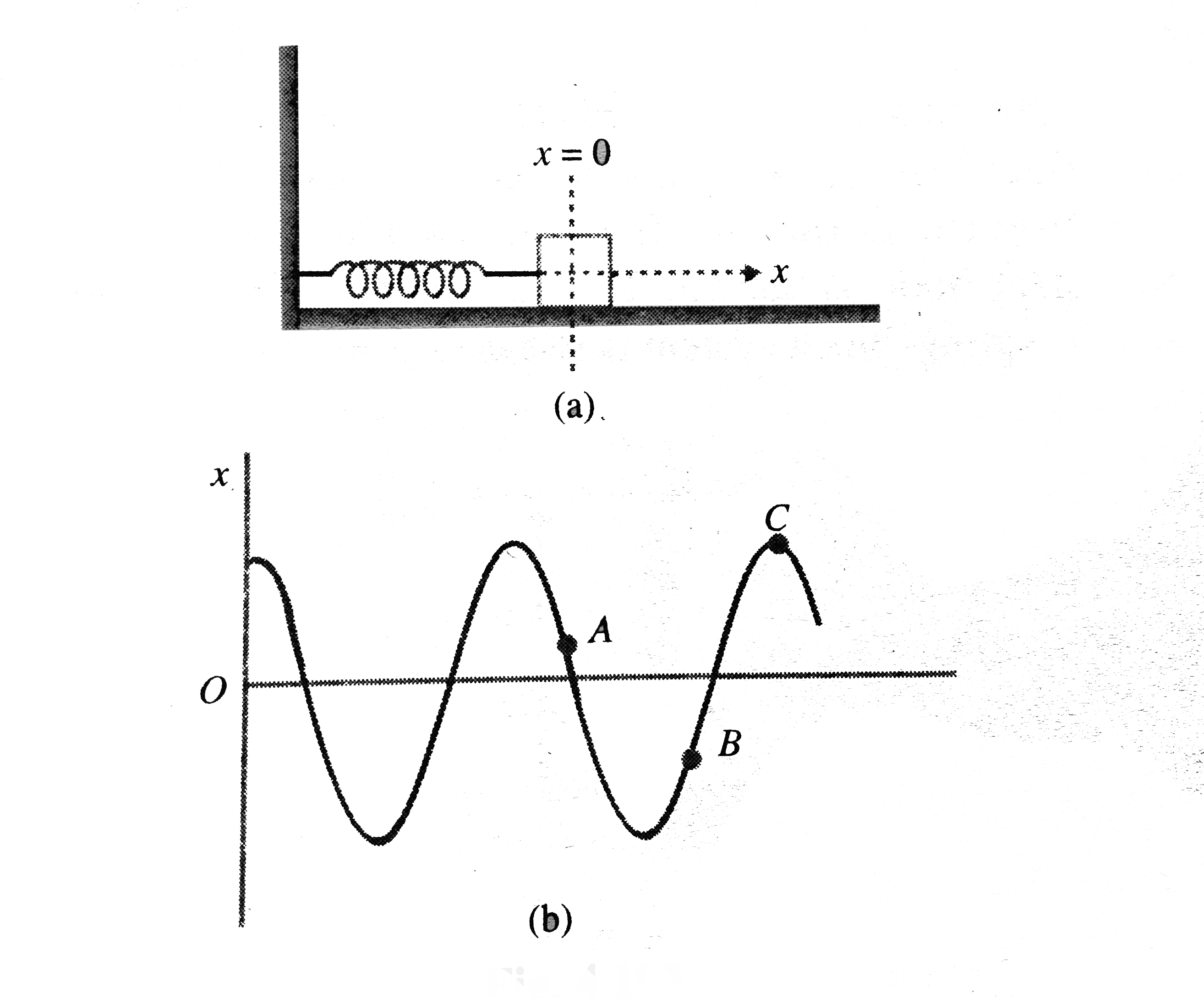
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed as
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

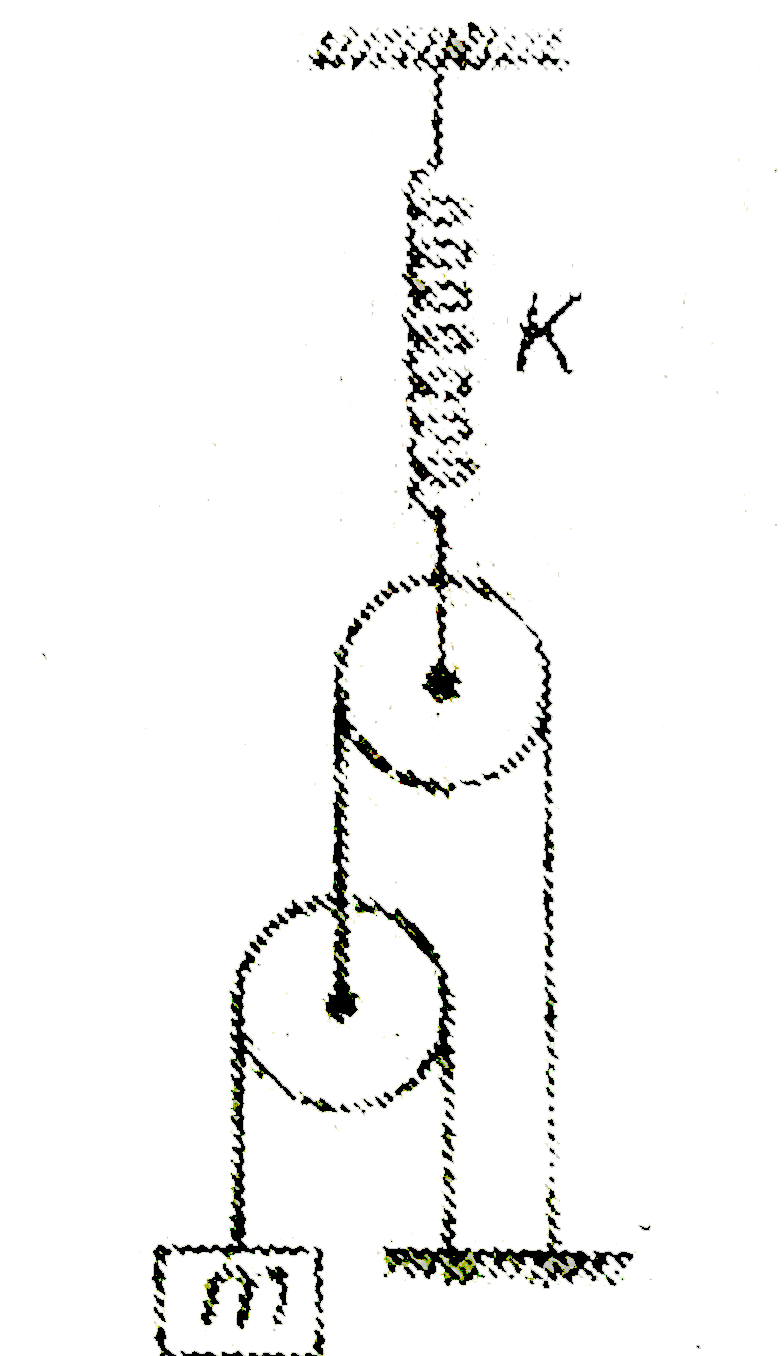
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
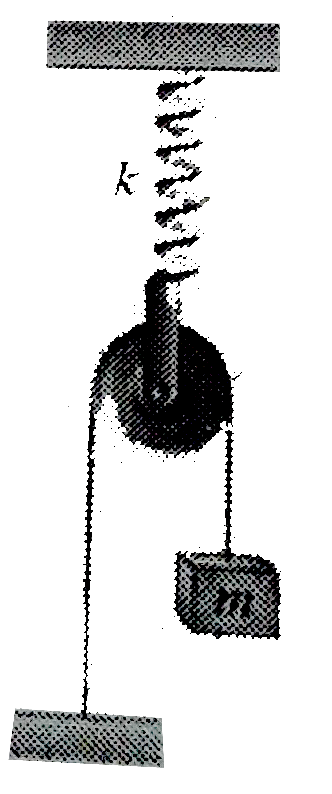
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be

View SolutionSpring of spring constant 1200Nm−1 is mounted on a smooth fricationless surface and attached to a block of mass 3kg. Block is pulled 2cm to the right and released. The angular frequency of oscillation is
_S01_037_Q01.png)
View Solution