STATEMENT-1 : Any oscillatory motion cannot be treated as simple harmonic.
STATEMENT-2 : Even under larger amplitude restoring force should be proportional to displacement for being classified as SHM.
Statement-1 is True, Statement-2 is True , Statement-2 is a corrrect explanation for Statement-1
Statement-1 is True, Statement-2 is True , Statement-2 is NOT a corrrect explanation for Statement-1
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.
The correct Answer is:B
To analyze the given statements, we will break down the concepts of oscillatory motion and simple harmonic motion (SHM).
Step 1: Understanding Statement 1
Statement 1: Any oscillatory motion cannot be treated as simple harmonic.
- Explanation: This statement is true. Not all oscillatory motions qualify as simple harmonic motion. For a motion to be classified as SHM, it must satisfy specific criteria, particularly that the restoring force acting on the object must be directly proportional to the negative of its displacement from the equilibrium position.
Step 2: Understanding Statement 2
Statement 2: Even under larger amplitude, the restoring force should be proportional to displacement for being classified as SHM.
- Explanation: This statement is also true. For a motion to be classified as SHM, the restoring force must always be proportional to the displacement from the equilibrium position, regardless of the amplitude of the oscillation. This means that even if the amplitude is large, the relationship between the restoring force and displacement must still hold true (F = -kx, where k is a constant).
Step 3: Conclusion
- Both statements are true. However, Statement 2 does not provide a correct explanation for Statement 1. While Statement 1 correctly asserts that not all oscillatory motions are SHM, Statement 2 simply reiterates a condition for SHM without explaining why some oscillatory motions do not qualify as SHM.
Final Answer:
- Statement 1 is true.
- Statement 2 is true but does not explain Statement 1.
Statement 1: Any oscillatory motion cannot be treated as simple harmonic.
Statement 2: Even under larger amplitude, the restoring force should be proportional to displacement for being classified as SHM.
- Both statements are true. However, Statement 2 does not provide a correct explanation for Statement 1. While Statement 1 correctly asserts that not all oscillatory motions are SHM, Statement 2 simply reiterates a condition for SHM without explaining why some oscillatory motions do not qualify as SHM.
- Statement 1 is true.
- Statement 2 is true but does not explain Statement 1.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (1)
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (2)
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Match The Column
9 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
STATEMENT-1 : An oscillatory motion is necessarily periodic.
and
STATEMENT -2 : A simple harmonic motion is necessarily osciallatory.
View SolutionCan simple harmonic motion take place in a non inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
View SolutionSTATEMENT-1: If a body is floacting submerged,then on pressing, it will execute damped oscillatory motion.
and
STATEMENT-2: When a body is floating fully submerged and displaced from its position , then no net force acts at its position.
View SolutionSTATEMENT 1: When a negative charge -q is released at a distance R from the centre and along the axis of a uniformly and positvely charged fixed ring of radius R, the negative charge does oscillation but not SHM. STATEMENT 2: The force on negative charge is always towards the centre of the ring but it is not proportional to the displacement from the centre of the ring.
View SolutionStatement-1 : The motion of a simple pendulum is not simple harmonic for large amplitudes.
Statement-2 : The restoring torque on a simple pendulum about the point of suspension is proportional to sinθ, where θ is the angular displacement of the pendulum.
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
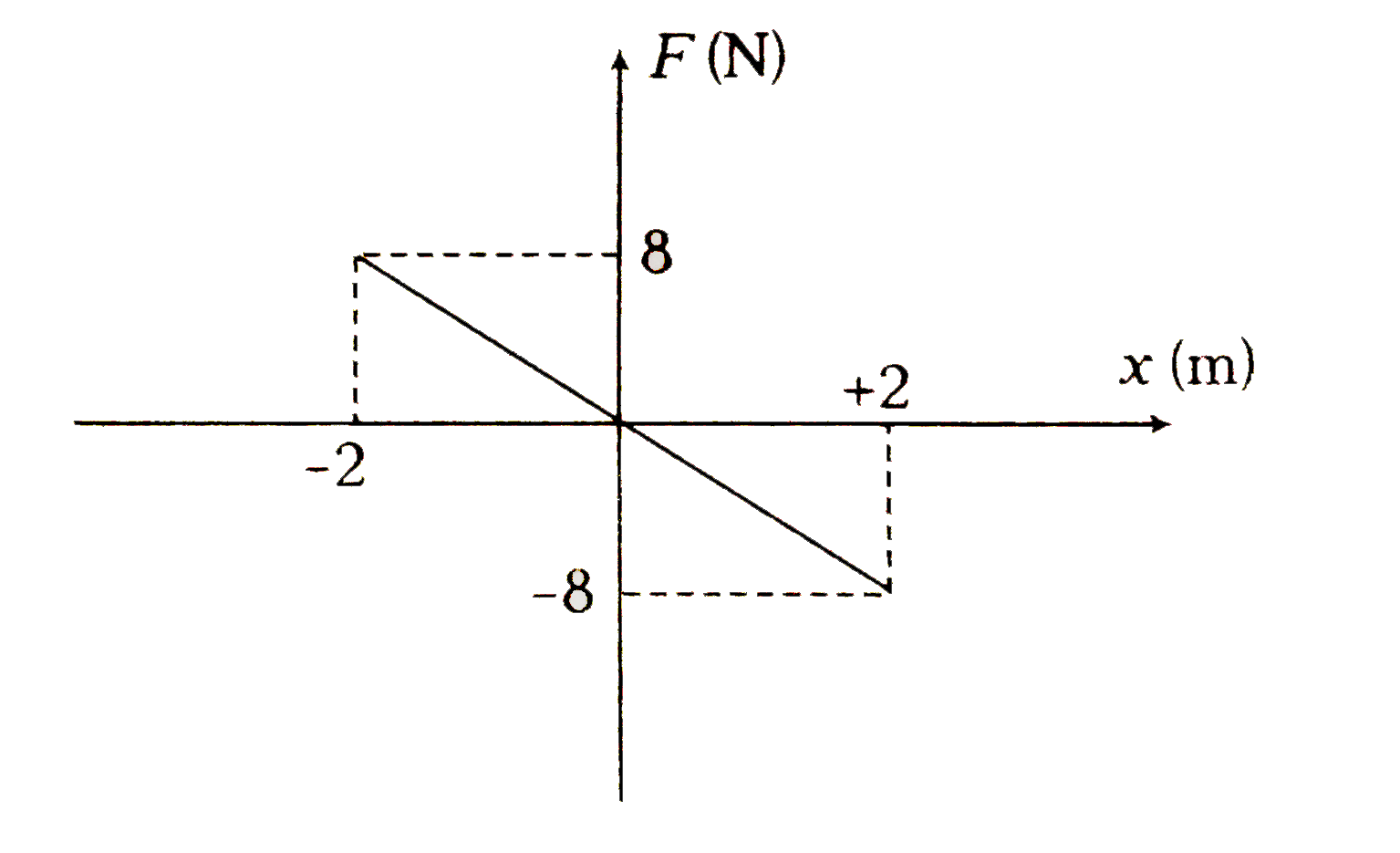
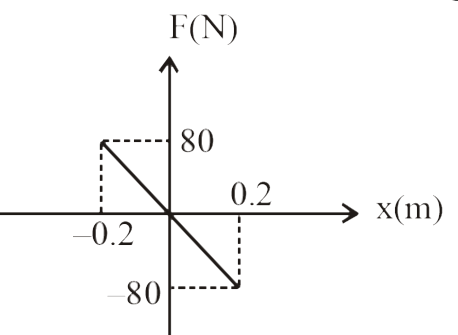
View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
View SolutionSTATEMENT-1: In SHM the scalar product of velocity and acceleration is always negative .
STATEMENT-2 : Time period of a simple pendulum of very large lenth compared to earth's radius is 1.4 hr.
STATEMENT-3 : For a given amplitude of S.H.M. total energy of spring mass system is independent of mass of body.
View SolutionSTATEMENT-1 Work done by a force depends on the frame of reference.
STATEMENT-2 Displacement of a body is different in different frames of reference.
View SolutionSTATEMENT-1 : Charge cannot exist without matter.
STATEMENT-2 : Charge of body depends on its velocity.
STATEMENT -3 : The charge cannot exert force on itself.
View Solution
