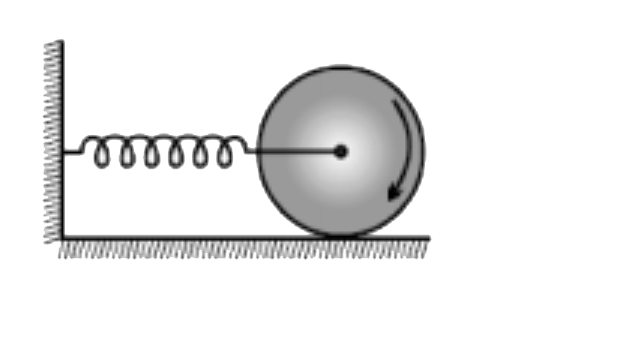
Passage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.
f versus t (time) graph will be as
_E01_082_O01.png)
_E01_082_O02.png)
_E01_082_O03.png)
_E01_082_O04.png)
The correct Answer is:C
_E01_082_S01.png)
kx−f=ma,fR=(mR22)α=f=13kx
But x=Acosωt
(∴ the cylinder is starting from x=A)
So f=kA3cosωt
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (3)2videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (4)2videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (1)2videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. Then choose the correct option(s)
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
View Solution
Knowledge Check
- Question 1 - Select One
Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
A2Mr2B3Mr2C4Mr2D5Mr2
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.
Force of friction between the disc and the plank isView SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
View SolutionA disc of mass M and radius R has a spring of constant k attached to its center , the other end of the spring being fixed to a vertical wall. If the disk rolls without slipping on a level floor, how far to the right does the centre of mass move , if Initially the spring was unstretched and the angular speed of the disc was ω0
View SolutionA disc of radius R and mass M is under pure rolling under the action of a force F applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
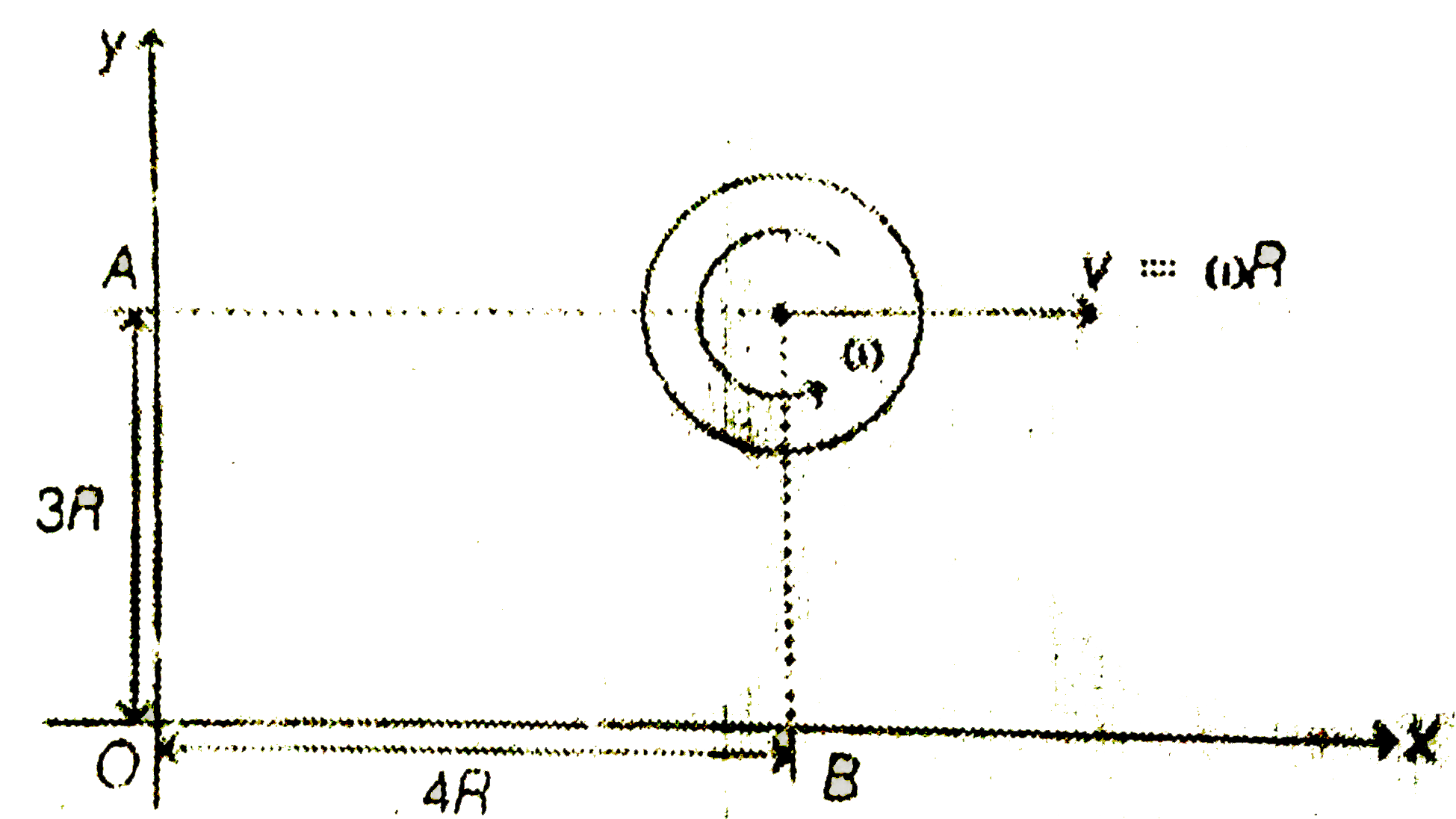View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.
Acceleration of the plank isView SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc
View Solution