A radioactivity decay is given by
Only A is present at . Find the time at which if we are able to pick one atom out of the sample, then probability of getting B is getting a.
To solve the problem step by step, we will use the concepts of radioactive decay and probability.
Step 1: Understand the problem
We have a radioactive decay process where substance A decays into substance B. The half-life of A is given as 8 years. At time t=0, only substance A is present.
Step 2: Define the probabilities
We need to find the time t at which the probability of picking an atom of substance B is 15 times the probability of picking an atom of substance A.
Let:
- N0 = initial number of atoms of A at t=0
- N = number of atoms of A remaining at time t
- NB = number of atoms of B formed at time t
Since A decays into B, we have:
NB=N0−N
Step 3: Write the probabilities
The probability of picking an atom of A is:
P(A)=NN0
The probability of picking an atom of B is:
P(B)=NBN0=N0−NN0
Step 4: Set up the equation
According to the problem:
P(B)=15×P(A)
Substituting the expressions for probabilities:
N0−NN0=15×NN0
Step 5: Simplify the equation
Multiplying both sides by N0 gives:
N0−N=15N
N0=16N
Step 6: Relate N to N0 using decay formula
The number of remaining atoms of A after time t can be expressed using the half-life formula:
N=N0(12)tt1/2
where t1/2=8 years.
Step 7: Substitute N in the equation
Substituting N in the equation N0=16N:
N0=16⎛⎝N0(12)t8⎞⎠
1=16(12)t8
Step 8: Solve for t
Rearranging gives:
(12)t8=116
Since 116=(12)4, we have:
t8=4
Thus,
t=32 years
Final Answer
The time at which the probability of getting B is 15 times that of getting A is 32 years.
---
We have a radioactive decay process where substance A decays into substance B. The half-life of A is given as 8 years. At time t=0, only substance A is present.
We need to find the time t at which the probability of picking an atom of substance B is 15 times the probability of picking an atom of substance A.
- N0 = initial number of atoms of A at t=0
- N = number of atoms of A remaining at time t
- NB = number of atoms of B formed at time t
NB=N0−N
The probability of picking an atom of A is:
P(A)=NN0
P(B)=NBN0=N0−NN0
According to the problem:
P(B)=15×P(A)
N0−NN0=15×NN0
Multiplying both sides by N0 gives:
N0−N=15N
N0=16N
The number of remaining atoms of A after time t can be expressed using the half-life formula:
N=N0(12)tt1/2
where t1/2=8 years.
Substituting N in the equation N0=16N:
N0=16⎛⎝N0(12)t8⎞⎠
1=16(12)t8
Rearranging gives:
(12)t8=116
Since 116=(12)4, we have:
t8=4
Thus,
t=32 years
The time at which the probability of getting B is 15 times that of getting A is 32 years.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 021videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 032videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Nuclear Physics : Solved Example5videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A and B are moving in two circular orbits with angular velocity
2ωandω respectively. Their position are shown at t = 0. Find the time at which they will meet for 1st time
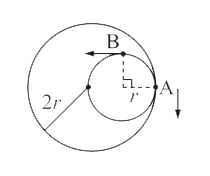 View Solution
View SolutionTwo radioactive samples of different elements (half-lives t1 and t2 respectively) have same number of nuclei at t=0. The time after which their activities are same is
View Solution
Knowledge Check
- Question 1 - Select One
Two radioactive substance A and B have decay constants 5λ and λ respectively. At t=0 they have the same number of nuclei. The ratio of number of nuclei of nuclei of A to those of B will be (1e)2 after a time interval
A14λB4λC2λD12λ
There are two radio nuceli A and B.A is an α emitter and B a β emitter. Their disintegration constant are in the ratio of 1:2 What should be the ratio of number of atoms of A and B at any time t so that probabilities of getting alpha and beta particles are same at that instant?
View SolutionGraph of velocity (v) versus time 't' for motion of a motorbike which starts from rest and moves along a stright road is given .
(a)Find the average acceleration for the time interval t0=0 to t1=6.0 s
(b) Estimate the time at which the acceleration has its greatest positive value and the value of the acceleration at that instant.
(c) When is the acceleration is zero ?
(d) Estimate the maximum negative value of the acceleration and the time at which it occurs.
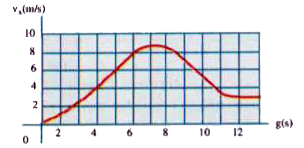 View Solution
View SolutionA radioactive nucleus A with a half life T, decays into nucleus B. At t=0, there is no nucleus B. At some time t, the ratio of the number of B to that of A is 0.3 . Then, t is given by
View SolutionThe displacement of a body at any time t after starting is given by s=15t−0.4t2. Find the time when the velocity of the body will be 7ms−1.
View SolutionThe XIth class students of ALLEN designed a rocket. The rocket was launched from cycle stand of ALLEN straight up into the air. At t=0, the rocket is at y=0 with Vy(t=0)=0. The velocity of the rocket is given by: Vy=(24t−3t2)m/s for 0≤t≤tb where tb is the time at which fuel burns out. vertically upward direction is taken as positive. (g=10m/s2)
The displacement of the rocket till the fuel burns out (t=tb) isView SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
If vapours are collected in a container of volume 8.21L maintained at 3T/2K, where T=50K, then the ratio of initial rate of effusion of gases A and B is given asView SolutionTwo radioactive substances A and B have decay constants 5λ and λ respectively. At t=0 , they have the same number of nuclei. The ratio of number of nuclei of A of those of B will be (1/e)2 after a time interval
View Solution

