The XIth class students of ALLEN designed a rocket. The rocket was launched from cycle stand of ALLEN straight up into the air. At t=0, the rocket is at y=0 with Vy(t=0)=0. The velocity of the rocket is given by: Vy=(24t−3t2)m/s for 0≤t≤tb where tb is the time at which fuel burns out. vertically upward direction is taken as positive. (g=10m/s2)
The displacement of the rocket till the fuel burns out (t=tb) is
128 m
486m
203m
242m
To find the displacement of the rocket until the fuel burns out, we need to follow these steps:
Step 1: Determine the time at which the fuel burns out (t_b)
The velocity of the rocket is given by the equation:
Vy=24t−3t2
To find the time tb when the fuel burns out, we need to find the maximum velocity. This occurs when the derivative of the velocity with respect to time is zero.
Taking the derivative:
dVydt=24−6t
Setting the derivative equal to zero to find the critical points:
24−6t=0
6t=24
t=4 seconds
Thus, tb=4 seconds.
Step 2: Calculate the maximum velocity at tb
Now, we can calculate the maximum velocity at t=tb:
Vy(tb)=24(4)−3(42)
Vy(tb)=96−48
Vy(tb)=48 m/s
Step 3: Calculate the displacement until tb
The displacement s can be found by integrating the velocity function from t=0 to t=tb:
s=∫tb0Vydt=∫40(24t−3t2)dt
Calculating the integral:
s=∫40(24t−3t2)dt
=(12t2−t3)40
=(12(42)−(43))−(12(02)−(03))
=(12⋅16−64)−0
=192−64
=128 meters
Final Answer
The displacement of the rocket until the fuel burns out is:
128 meters
---
The velocity of the rocket is given by the equation:
Vy=24t−3t2
To find the time tb when the fuel burns out, we need to find the maximum velocity. This occurs when the derivative of the velocity with respect to time is zero.
dVydt=24−6t
24−6t=0
6t=24
t=4 seconds
Thus, tb=4 seconds.
Now, we can calculate the maximum velocity at t=tb:
Vy(tb)=24(4)−3(42)
Vy(tb)=96−48
Vy(tb)=48 m/s
The displacement s can be found by integrating the velocity function from t=0 to t=tb:
s=∫tb0Vydt=∫40(24t−3t2)dt
s=∫40(24t−3t2)dt
=(12t2−t3)40
=(12(42)−(43))−(12(02)−(03))
=(12⋅16−64)−0
=192−64
=128 meters
The displacement of the rocket until the fuel burns out is:
128 meters
Topper's Solved these Questions
Similar Questions
The XIth class students of ALLEN designed a rocket. The rocket was launched from cycle stand of ALLEN straight up into the air. At t=0, the rocket is at y=0 with Vy(t=0)=0. The velocity of the rocket is given by: Vy=(24t−3t2)m/s for 0≤t≤tb where tb is the time at which fuel burns out. vertically upward direction is taken as positive. (g=10m/s2)
The time taken for rocket to reach its maximum height isView SolutionThe XIth class students of ALLEN designed a rocket. The rocket was launched from cycle stand of ALLEN straight up into the air. At t=0, the rocket is at y=0 with Vy(t=0)=0. The velocity of the rocket is given by: Vy=(24t−3t2)m/s for 0≤t≤tb where tb is the time at which fuel burns out. vertically upward direction is taken as positive. (g=10m/s2)
The expression for the acceleration ay(t) valid at all times in the interval 0<t<tb isView Solution
Knowledge Check
- Question 1 - Select One
The position of particle at time t is given by, x(t)=(v0/∝)(1−e−ut) where v0 is a constant ∝>0. The dimension of v0 and ∝ are,
AM0LT−1andT−1BM0LT0andT−1CM0LT−1andLT−2DM0LT−1andT
A particle thrown up vertically from the ground at reaches its highest point at t=t0 =The displacement of the particle between t=7t08andt=t0 is S. Then u2Sg=
View SolutionFind the average speed of a particle whose velocity is given by V=V0sinωt t where T=2π/ω is the time of complete cycle
View SolutionThe velocity (v)-time (t) graph of a partide moving along a straight line is as shown in the figure. The displacement of the particle from t = 0 to t = 4 is
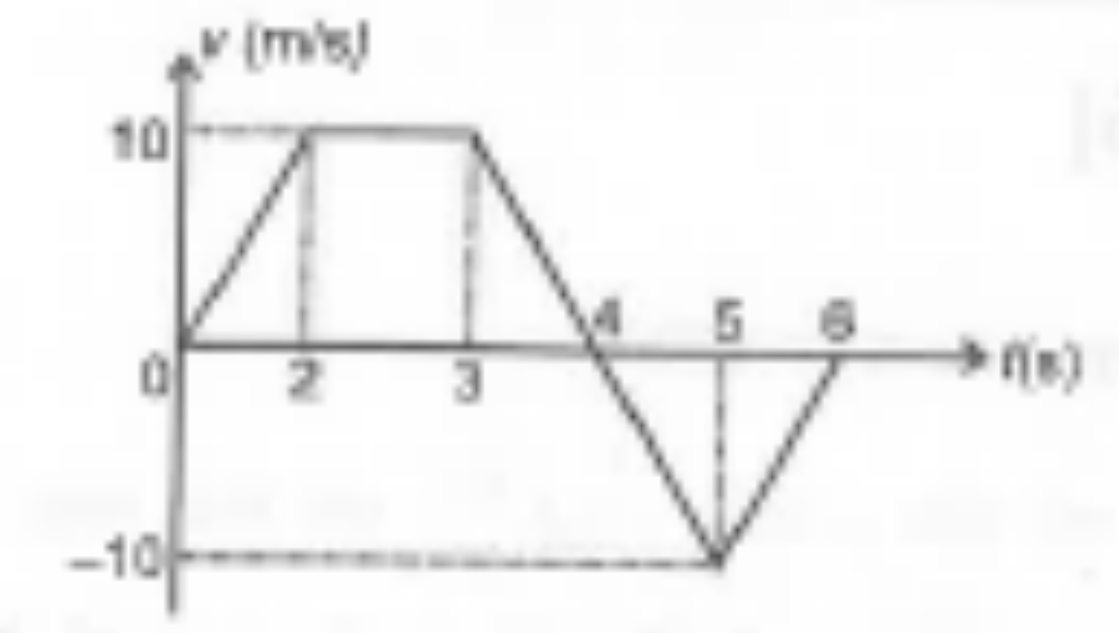 View Solution
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionA rocket of initial mass m0 has a mass m0(1−t/3) at time t. The rocket is lauched from rest vertically upwards under gravity and expels burnt fuel at a speed u relative to the rocket vertically downward. Find the speed of rocket at t=1.
View SolutionA ball is projected from origin at time t= 0. The x and A y coordinates of its displacement are given by (x=4t2) and y = (3t - 5). Then its instantaneous velocity at any time t is
View Solution

