Starting with a sample of pure 66Cu,78 of it decays into Zn in 15 min. The corresponding half-life is
10 min
15 min
5 min
712 min
The correct Answer is:C
We know that, NN0=(12)n where, N are the radioactive nuclei left after n-half lives N0 are the initial number of nuclei and n is number of half-lives,
N0/8N0=18=(12)3=(12)n⇒n=3
Therefore T1/2=153=5 min
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Knowledge Check
Radioactive carbon dating can determine how long ago an organism lived by measuring how much of thte 14C in the sample has decayed. 14C is an isotope of carbon that has a half-life of 5,600 years.Half-life is the amount of time it takes for half of the original amount to decay. If a sample of a petrified tree contains 6.25 percent of its original 14C, how long ago did the tree die ?
A22,400 yearsB28,000 yearsC35,000 yearsD89,600 yearsA fraction f1 of a radioactive sample decays in one mean life, and a fraction f2 decays in one half life. Then
Af1>f2Bf1<f2Cf1=f2Deither of (a),(b ) or (c ) depending on the values of the mean life and half life.
8 kg of Cu66 undergones radioactive decay and after 15 minutes only 1 kg remains . The half - life , in minutes , is then
View SolutionThe half life of 2g sample of radioactive nuclide 'X' is 15 min. The half life time of 1g sample of X is
View SolutionA bone containing 200g carbon-14 has β-decay rate of 375 decay/min. Calculate the time that has elapsed since the death of the living one. Given the rate of decay for the living organism is equal to 15 decay per min per gram of carbon and half-life of carbon-14 is 5730years.
View SolutionA bone containing 200 g carbon-14 has β-decay rate of 375 decay/min. Calculate the time that has elapsed since the death of the living one. Given the rate of decay for the living organism is equal to 15 decay per min per gram of carbon and half-life of carbon-14 is 5730 years.
View SolutionThe probability that particular nucleus of 38Cl will undergo β-decay in time interval 10−3 sec (the half life of 38Cl is 37.2 min) is
View SolutionThe graph represents the decay of a newly-prepared sample of radioactive nuclide X to a stable nuclide Y. The half-life of X is t. The growth curve for Y intersects the decay curve for X after time T. What is the time T ?
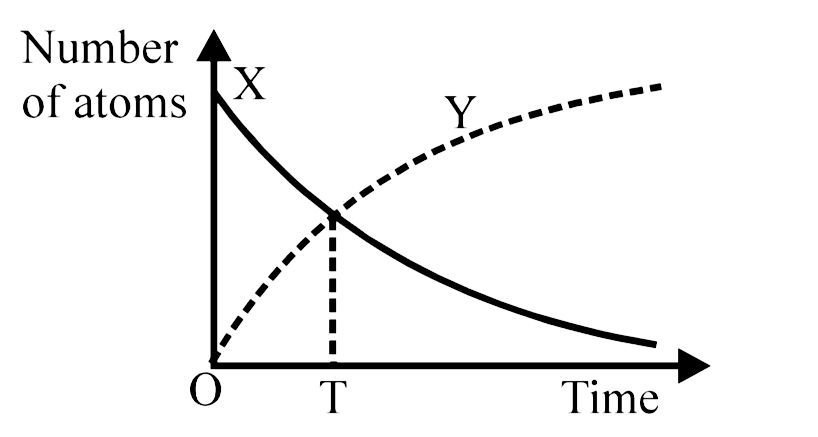
View Solution
