After absobing a slowly moving neutron of mass mN (mometum ~0), a nucleus of mass M breaks into two nuclei of masses m1and5m1(6m1=M+mN), respectively. If the de - Broglie wavelength of the nucleus with mass m1 is λ, then de - Broglie wavelength of the other nucleus will be
25λ
5λ
λ5
λ
The correct Answer is:D
_E01_267_S01.png)
According to Conservation of linear momentum P=P. Therefore λ'=λ
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]39videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]12videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]20videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
After absorbing a slowly moving neutrons of mass mN (momentum ~0) a nucleus of mass M breaks into two nucleii of mass m1and5m1(6m1=M+mN), respectively . If the de-Broglie wavelength of the nucleus with mass m1 is λ, then de Broglie wavelength of the other nucleus will be
View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
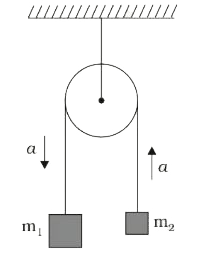 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
Atheir momenta are the same.Btheir energies are the same.Cmomentum of A1 is less than the momentum of A2.Denergy of A1 is more than the energy of A2. - Question 2 - Select One
A particle of mass 4m at rest decays into two particles of masses m and 3m having non-zero velocities. The ratio of the de Broglie wavelengths of the particles 1 and 2 is
A12B14C2D1
The de-Broglie wavelength of a particle with mass 1g and velocity 100m/sec is.
View SolutionA praticle of mass M at rest decays into two particle of masses m1 and m2, having non-zero velocities. The ratio of the de Broglie wavelength of the particles λ1λ2 is
View SolutionTwo particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
View SolutionA particle of mass 3m at rest decays into two particles of masses m and 2m having non-zero velocities. The ratio of the de Broglie wavelengths of the particles (λ1λ2) is
View SolutionThe de - Broglie wavelength associated with the particle of mass m moving with velocity v is
View SolutionThe atomic masses of He and Ne are 4 and 20 amu respectively . The value of the de Broglie wavelength of He gas at−73.∘C is ''M'' times that of the de Broglie wavelength of Ne at 727.∘C. M is
View Solution

