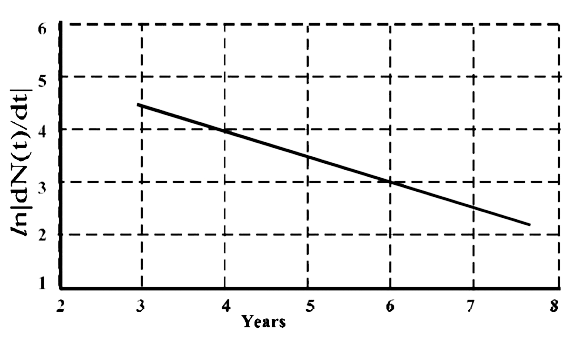
To determine the half life of a radioactive element , a student plot a graph of in $∣ ∣ ∣ \frac{d N (t)}{d t} ∣ ∣ ∣$ versus $t$ , Here $∣ ∣ ∣ \frac{d N (t)}{d t} ∣ ∣ ∣$ is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after $4.16$ year the value of p is

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $8$

$∣ ∣ ∣ \frac{d N}{d t} ∣ ∣ ∣ = λ N_{0} e^{- λ t} ∴ ln ∣ ∣ ∣ \frac{d N}{d t} ∣ ∣ ∣ = ln (N_{0} λ) - λ t$
$∴ ln ∣ ∣ ∣ \frac{d N}{d t} ∣ ∣ ∣ = ln (N_{0} λ) - λ t \Rightarrow - λ =$ slope $= - \frac{1}{2} y e a r^{- 1}$
$\Rightarrow λ = \frac{1}{2} y r^{- 1}$
$∴ t_{1 / 2} = \frac{0.693}{λ} = 1.386$ given time is $3$ times of $t_{1 / 2}$
$∴$ value of p is 8.

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Nuclei of a radioactive element $A$ are being produced at a constant rate $α$ . The element has a decay constant $λ$ . At time $t = 0$ , there are $N_{0}$ nuclei of the element.
(a) Calculate the number $N$ of nuclei of $A$ at time $t$ .
(b) If $α = 2 N_{0} λ$ , calculate the number of nuclei of A after one half-life of A, and also the limiting value of N as $t \to \infty$ .
A $\frac{1}{λ} [α + (α - N_{0} λ) e^{- λ t}]$
B $\frac{1}{λ} [α - (α - N_{0} λ) e^{- λ t}]$
C $λ [α - (α - N_{0} λ) e^{- λ t}]$
D $[α - (N_{0} λ - α) e^{- λ t}]$

ALLEN-SIMPLE HARMONIC MOTION-Subjective

Home
Ask Doubt
Profile