A circular platform rotates around a vertical axis with angular velocity ω=10rad/s. On the platform is a ball of mass 1kg, attached to the long axis of the platform by a thin of length of 10cm (α=30∘). Find normal force exerted by the ball on the platform (in newton). Friction is absent.
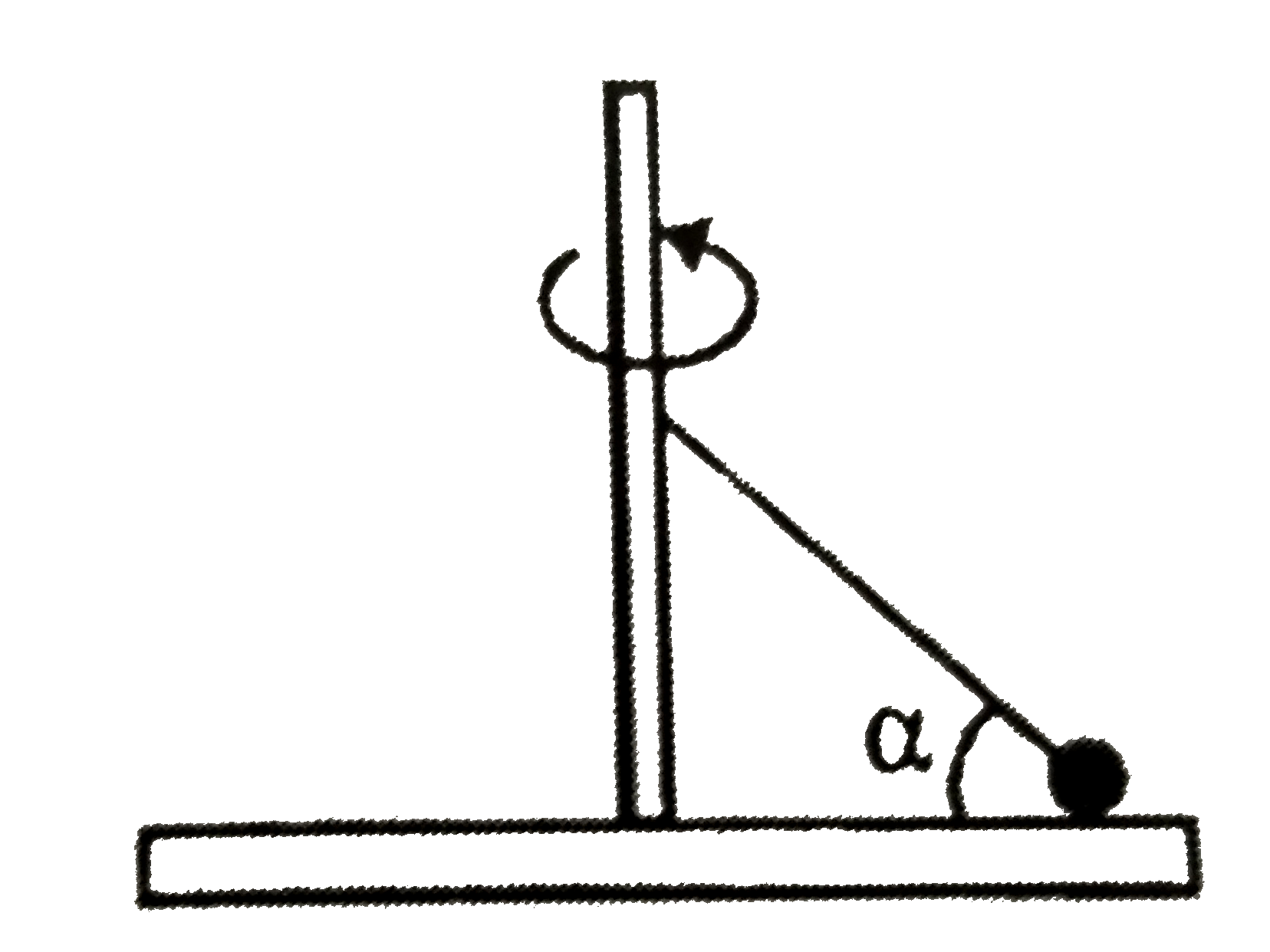
The correct Answer is:5
Step by step video & image solution for A circular platform rotates around a vertical axis with angular velocity omega=10rad//s. On the platform is a ball of mass 1kg, attached to the long axis of the platform by a thin of length of 10cm (alpha=30^(@)). Find normal force exerted by the ball on the platform (in newton). Friction is absent. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(S-2)
6 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)
22 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)
8 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions

A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity ω. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View Solution
Knowledge Check
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity of
Aω(M−2m)(M+2m)BωM(M+2m)CωM(M+m)Dω(M+2m)MA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω, Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity ω=
AωMM+mBω(M−2m)M+2mCωMM+2mDω(M+2m)M
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping a angular velocity ω. When it crosses point B disc will be in :
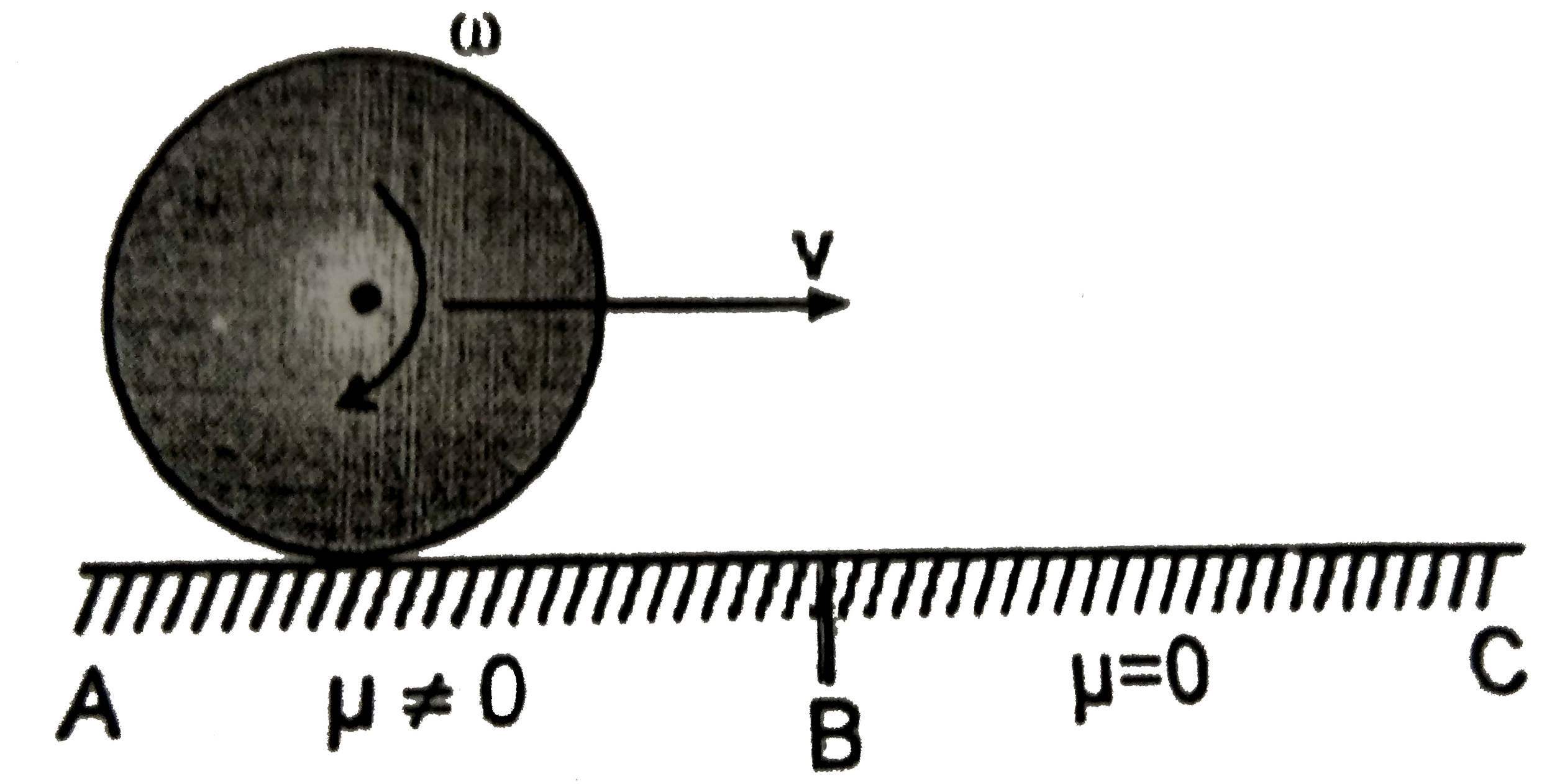
View SolutionA platform is moving upwards with an accelerations of 5ms−2. At the moment when its velocity is u=3ms−1, a ball is thrown from it with a speed of 30ms−1 w.r.t. platform at an angle of θ=30∘ with horizontal. The time taken by the ball to return to the platform is
View SolutionA rod of mass M and length l attached with a small bob of mass m at its end is freely rotating about a vertical axis passing through its other end with a constant angular speed ω. Find the force exerted by the system (rod and bob) on the pivot. Assume that gravity is absent.
View SolutionA whel of mass 2kg an radius 10 cm is rotating about its axis at an angular velocity of 2πrad/s the force that must be applied tangentially to the wheel to stop it in 5 revolutions is
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View Solution
