∣∣
∣
∣
∣
∣
∣
∣
∣∣List-I(Atom/Ions)List-II(Electron Affinity in eV/atom and consider that EA=−ΔHe.g)(P)F(1)3.4(Q)F+(2)17.4(R)Cl(3)13(S)Cl+(4)3.6∣∣
∣
∣
∣
∣
∣
∣
∣∣
Code :
(A+B+C) is an integer
(A+B+C) is an integer
(8A+2C)is an integer
A,BC are integers
The correct Answer is:A, B, C, D
To solve the equation 2a2+3b2=35 where a and b are integers, we will follow these steps:
Step 1: Rearranging the Equation
We start with the equation:
2a2+3b2=35
We will isolate b2:
3b2=35−2a2
b2=35−2a23
Step 2: Finding Integer Solutions
For b2 to be an integer, 35−2a2 must be divisible by 3. We will check values of a that keep b2 non-negative.
Step 3: Testing Integer Values for a
We will test integer values for a:
1. For a=0:
b2=35−2(0)23=353(not an integer)
2. For a=1:
b2=35−2(1)23=333=11(b=±√11 (not an integer))
3. For a=2:
b2=35−2(2)23=273=9(b=±3)
4. For a=3:
b2=35−2(3)23=233(not an integer)
5. For a=4:
b2=35−2(4)23=193(not an integer)
6. For a=5:
b2=35−2(5)23=53(not an integer)
7. For a=6:
b2=35−2(6)23=−73(not valid)
Step 4: Collecting Solutions
From our tests, we found valid pairs:
- (2,3)
- (2,−3)
- (−2,3)
- (−2,−3)
Step 5: Additional Valid Pairs
We can also check negative values for a:
- For a=−2, we get the same results as for a=2.
Final Count of Solutions
The valid integer pairs (a,b) are:
1. (2,3)
2. (2,−3)
3. (−2,3)
4. (−2,−3)
5. (4,1)
6. (4,−1)
7. (−4,1)
8. (−4,−1)
Thus, we have a total of 8 distinct pairs.
Conclusion
The total number of integer solutions is:
Answer: 8
We start with the equation:
2a2+3b2=35
We will isolate b2:
3b2=35−2a2
b2=35−2a23
For b2 to be an integer, 35−2a2 must be divisible by 3. We will check values of a that keep b2 non-negative.
We will test integer values for a:
b2=35−2(0)23=353(not an integer)
b2=35−2(1)23=333=11(b=±√11 (not an integer))
b2=35−2(2)23=273=9(b=±3)
b2=35−2(3)23=233(not an integer)
b2=35−2(4)23=193(not an integer)
b2=35−2(5)23=53(not an integer)
b2=35−2(6)23=−73(not valid)
From our tests, we found valid pairs:
- (2,3)
- (2,−3)
- (−2,3)
- (−2,−3)
We can also check negative values for a:
- For a=−2, we get the same results as for a=2.
The valid integer pairs (a,b) are:
1. (2,3)
2. (2,−3)
3. (−2,3)
4. (−2,−3)
5. (4,1)
6. (4,−1)
7. (−4,1)
8. (−4,−1)
The total number of integer solutions is:
Answer: 8
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:MATHEMATICS
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS SECTION-I
Explore 2 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:Chemistry
Explore 54 Videos
- SEQUENCE AND PROGRESSIONBook:ALLENChapter:SEQUENCE AND PROGRESSIONExercise:Exercise (JA)
Explore 12 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:PHYSICS
Explore 4 Videos
Similar Questions
Match List - I and List - II .
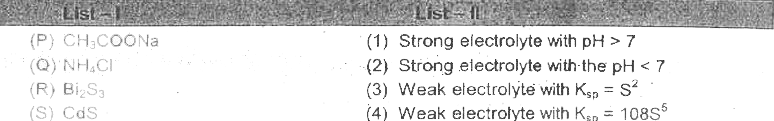
PQRS(A)4312(B)3421(C)4321(D)4231
View SolutionMatch the stoichiometric coefficients listed in Column II with the species listed in Column I that are involved in the balanced equation of the reaction :
LIST -ILIST -II(P)FeC2O4(1)10(Q)MnO−4(2)24(R)H+(3)5(S)CO2(4)3
View SolutionMatch List - I and List - II .

PQRS(A)4213(B)4132(C)1423(D)4123
View SolutionMatch Column - I with Column - II
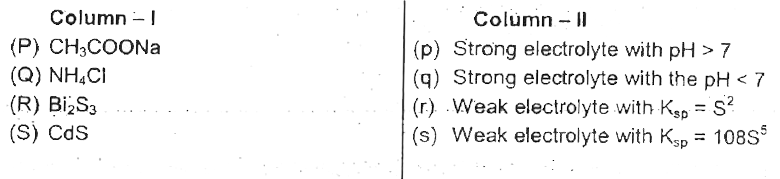
PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionThe standard reduction potential data at 25∘C is given below
E∘(Fe3+,Fe2+)=+0.77V,
E∘(Fe2+,Fe)=−0.44V,
E∘(Cu2+,Cu)=+0.34V,
E∘(Cu+,Cu)=+0.52V,
E∘(O2(g)+4H++4e−→2H2O]=+1.23V
E∘[(O2(g)+2H2O+4e−→4OH−)]=+0.40V,
E∘(Cr3+,Cr)=−0.74V,
E∘(Cr2+,Cr)=−0.91V,
Match E∘ of the redox pair in List-I with the values given in List-II and select the correct answer using the code given below teh lists:
List−IList−II(P)E∘(Fe3+,Fe)(1)−0.18V(Q)E∘(4H2O⇔4H++4OH+)(2)−0.4V(R)E∘(Cu2++Cu→2Cu+)(3)−0.04V(S)E∘(Cr3+,Cr2+)(4)−0.83V
Codes:
View SolutionThe standard reduction potential data at 25∘C is given below
E∘(Fe3+,Fe2+)=+0.77V,
E∘(Fe2+,Fe)=−0.44V,
E∘(Cu2+,Cu)=+0.34V,
E∘(Cu+,Cu)=+0.52V,
E∘(O2(g)+4H++4e−→2H2O]=+1.23V
E∘[(O2(g)+2H2O+4e−→4OH−)]=+0.40V,
E∘(Cr3+,Cr)=−0.74V,
E∘(Cr2+,Cr)=−0.91V,
Match E∘ of the redox pair in List-I with the values given in List-II and select the correct answer using the code given below the lists:
List−IList−II(P)E∘(Fe3+,Fe)(1)−0.18V(Q)E∘(4H2O⇔4H++4OH−)(2)−0.4V(R)E∘(Cu2++Cu→2Cu+)(3)−0.04V(S)E∘(Cr3+,Cr2+)(4)−0.83V
Codes:
View SolutionMatch list - I with list - II and select the correct answer using the codes given below :
List IList II(P)Schottky defect(1)NaCl+SrCl2(Q)Frenkel defect(2)Reating Na with Cl2(R)F - centres(3)NaCl(S)Metal deficiency(4)AgCl
View SolutionList -I SaltList -II Ksp(A)AgCIP.27S4(B)PbI2Q.108(S)5(C)AS2S3R.4S3(D)Ag3PO4S.S2
View SolutionSome relations and laws related to fluids are given in List - I , while the physical reasons behind them are given in List - II.

PQRS(A)2314(B)2431(C)4123(D)2344
View SolutionList-I List-II In the aqueous medium the ion can be(A)HPO−24P.Arrhenius acid(B)CO−23Q.Bronstead base(C)H2PO−13R.Amphoteric(D)H2PO−12S.Bronstead acid
View Solution