List -I SaltList -II Ksp(A)AgCIP.27S4(B)PbI2Q.108(S)5(C)AS2S3R.4S3(D)Ag3PO4S.S2
The correct Answer is:A-S;B-R;C-Q;D-P
To solve the problem of matching salts with their respective solubility products (Ksp), we need to analyze each salt's dissociation and calculate the Ksp based on its solubility. Let's go through each salt step by step.
Step 1: Analyze Silver Chloride (AgCl)
- Dissociation Reaction:
AgCl⇌Ag++Cl−
- Let the solubility (s) = s mol/L.
- Concentration of ions:
- (Ag+)=s
- (Cl−)=s
- Ksp Calculation:
Ksp=(Ag+)(Cl−)=s⋅s=s2
- Match: This corresponds to option S (Ksp = 27s^4).
Step 2: Analyze Lead(II) Iodide (PbI2)
- Dissociation Reaction:
PbI2⇌Pb2++2I−
- Let the solubility (s) = s mol/L.
- Concentration of ions:
- (Pb2+)=s
- (I−)=2s
- Ksp Calculation:
Ksp=(Pb2+)(I−)2=s⋅(2s)2=s⋅4s2=4s3
- Match: This corresponds to option R (Ksp = 108s^5).
Step 3: Analyze Arsenic Sulfide (As2S3)
- Dissociation Reaction:
As2S3⇌2As3++3S2−
- Let the solubility (s) = s mol/L.
- Concentration of ions:
- (As3+)=2s
- (S2−)=3s
- Ksp Calculation:
Ksp=(As3+)2(S2−)3=(2s)2⋅(3s)3=4s2⋅27s3=108s5
- Match: This corresponds to option Q (Ksp = 4s^3).
Step 4: Analyze Silver Phosphate (Ag3PO4)
- Dissociation Reaction:
Ag3PO4⇌3Ag++PO3−4
- Let the solubility (s) = s mol/L.
- Concentration of ions:
- (Ag+)=3s
- (PO3−4)=s
- Ksp Calculation:
Ksp=(Ag+)3(PO3−4)=(3s)3⋅s=27s3⋅s=27s4
- Match: This corresponds to option P (Ksp = 4s^3).
Final Matches:
- A matches with S (AgCl - Ksp = s^2)
- B matches with R (PbI2 - Ksp = 4s^3)
- C matches with Q (As2S3 - Ksp = 108s^5)
- D matches with P (Ag3PO4 - Ksp = 27s^4)
Summary of Matches:
- A - S
- B - R
- C - Q
- D - P
- Dissociation Reaction:
AgCl⇌Ag++Cl−
- Let the solubility (s) = s mol/L.
- Concentration of ions:
- (Ag+)=s
- (Cl−)=s
- Ksp Calculation:
Ksp=(Ag+)(Cl−)=s⋅s=s2
- Match: This corresponds to option S (Ksp = 27s^4).
- Dissociation Reaction:
PbI2⇌Pb2++2I−
- Let the solubility (s) = s mol/L.
- Concentration of ions:
- (Pb2+)=s
- (I−)=2s
- Ksp Calculation:
Ksp=(Pb2+)(I−)2=s⋅(2s)2=s⋅4s2=4s3
- Match: This corresponds to option R (Ksp = 108s^5).
- Dissociation Reaction:
As2S3⇌2As3++3S2−
- Let the solubility (s) = s mol/L.
- Concentration of ions:
- (As3+)=2s
- (S2−)=3s
- Ksp Calculation:
Ksp=(As3+)2(S2−)3=(2s)2⋅(3s)3=4s2⋅27s3=108s5
- Match: This corresponds to option Q (Ksp = 4s^3).
- Dissociation Reaction:
Ag3PO4⇌3Ag++PO3−4
- Let the solubility (s) = s mol/L.
- Concentration of ions:
- (Ag+)=3s
- (PO3−4)=s
- Ksp Calculation:
Ksp=(Ag+)3(PO3−4)=(3s)3⋅s=27s3⋅s=27s4
- Match: This corresponds to option P (Ksp = 4s^3).
- A matches with S (AgCl - Ksp = s^2)
- B matches with R (PbI2 - Ksp = 4s^3)
- C matches with Q (As2S3 - Ksp = 108s^5)
- D matches with P (Ag3PO4 - Ksp = 27s^4)
- A - S
- B - R
- C - Q
- D - P
Similar Questions
Knowledge Check
Match the column I with column II and mark the appropriate choice.
Column IColumn II(A)Fe(OH)3(i)Ksp=s2(B)Ag2CrO4(ii)Ksp=27s4(C)CH3COOAg(iii)Ksp=108s5(D)Ca3(PO4)(iv)Ksp=4s3A(A)→(iii),(B)→(ii),(C)→(iv),(D)→(i)B(A)→(ii),(B)→(iv),(C)→(i),(D)→(iii)C(A)→(i),(B)→(iii),(C)→(ii),(D)→(iv)D(A)→(iv),(B)→(i),(C)→(iii),(D)→(ii)
Match the stoichiometric coefficients listed in Column II with the species listed in Column I that are involved in the balanced equation of the reaction :
LIST -ILIST -II(P)FeC2O4(1)10(Q)MnO−4(2)24(R)H+(3)5(S)CO2(4)3
View SolutionMatch List-I with List-II and chose the correct answer from the code
List-I ElectrolyteList-I Solubility producta.Bi2S3i.4s3b.CdSii.27s2c.AI(OH)3iii.108s5d.CaF2iv.s2
View SolutionMatch List - I and List - II .
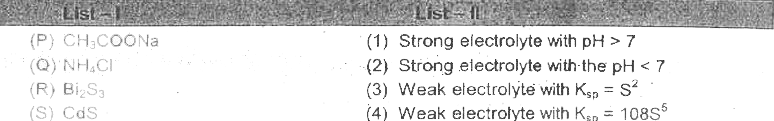
PQRS(A)4312(B)3421(C)4321(D)4231
View SolutionMatch List - I and List - II .

PQRS(A)4213(B)4132(C)1423(D)4123
View SolutionMatch List I and List II and select the correct answer using the code given below the lists :
List-I (reaction)List-II(equivelent weight)(A)FeS2→Fe+3+SO2(p)M/22(B)Fe2S3→2FeSO4+SO2(q)M/5(C)KMnO4in acidic medium(r)M/8(D)Cu2S→Cu2++SO2(s)M/11
View SolutionMatch the following :
Column-IColumn-II(A)3s1(p)n=3(B)3p1(q)l=0(C)4s1(r)l=1(D)4d1(s)m=0(t)m=±1
View SolutionList-I List-II In the aqueous medium the ion can be(A)HPO−24P.Arrhenius acid(B)CO−23Q.Bronstead base(C)H2PO−13R.Amphoteric(D)H2PO−12S.Bronstead acid
View Solution
