The speed(v) of a particle moving along a straight line is given by where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
(i) Here So,
Therefore
(ii) Here So
Therefore,
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exersice-037videos
BASIC MATHS
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - ASSERTION-REASON11videos
BASIC MATHS
- BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS40videos
AIIMS 2019
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
Similar Questions
The velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The speed is minimum after t=0 second at instant of timeView SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
View SolutionVelocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
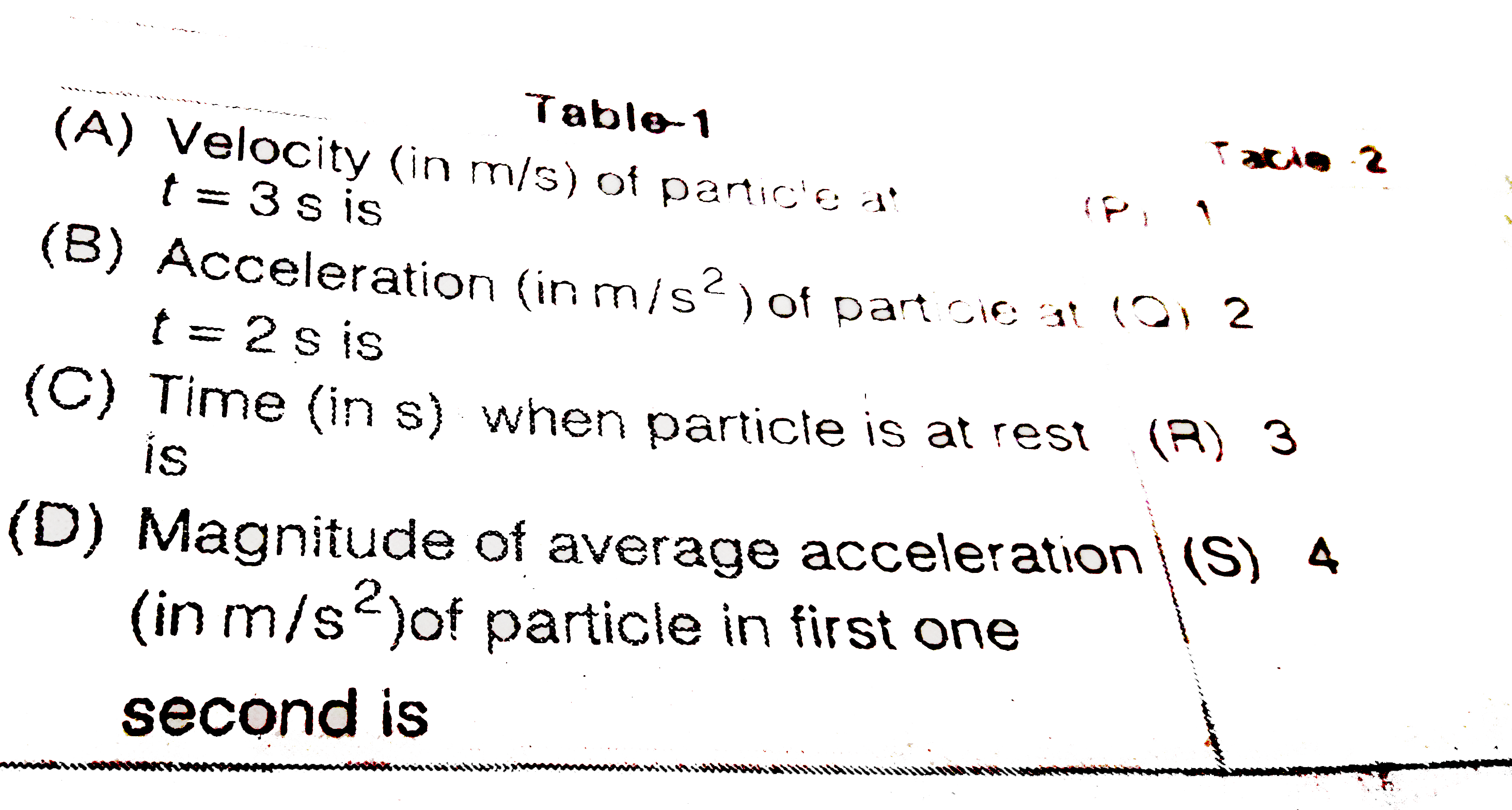 View Solution
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.View SolutionIf the particle is moving along a straight line given by the relation x=2−3t+4t3 where s is in cms., and t in sec. Its average velocity during the third sec is
View SolutionThe acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
View SolutionThe speed (v) and time (t) for an object moving along straight line are related as t2+400=4vt where v is in meter/second and t is in second. Find the possible positive values of v.
View Solution

