The resultant of A and B is R1 On reversing the vector B , the resultant R2 what is the value of R21+R22?
The correct Answer is:(3ˆi+94ˆj+4ˆk)m/s
→v=Aˆi+(3Bt2−2)ˆj+(2ct−4)ˆk
At t=2,Aˆi+(12B−2)ˆj+(4c−4)ˆk=3ˆi+22ˆj
Thus, A=3,B=2,C=1
∴Vec(v)=3ˆi+(6t2−2)ˆj+(2t−4)ˆk
At t=4,→v=3ˆi+(96−2)ˆj+(8−4)ˆk=3ˆi+94ˆj+4ˆk
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-5(A)15videos
BASIC MATHS
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exersice -05(B)20videos
BASIC MATHS
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exercise-04 [A]27videos
BASIC MATHS
- BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS40videos
AIIMS 2019
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
Similar Questions
The resultant vector of →P and →Q is →R. On reversing the direction of →Q the resultant vector becomes →S. Show that R2+S2=2(P2+Q2)
View SolutionThe resistance of metal sheet 1 between A and B is R1 and the resistance of sheet 2 between A' and B' is R2. The value of the ratio R1R2 is
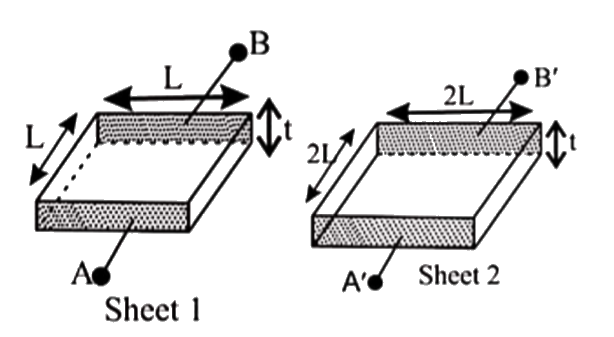 View Solution
View SolutionThe circuit is shown in the following figure. The potential at points A, B, C, D and O are given. The currents in the resistance R1,R2 and R3 are in the ratio of 4:2:1. What is the ratio of resistance R1,R2,R3 and R4 ?
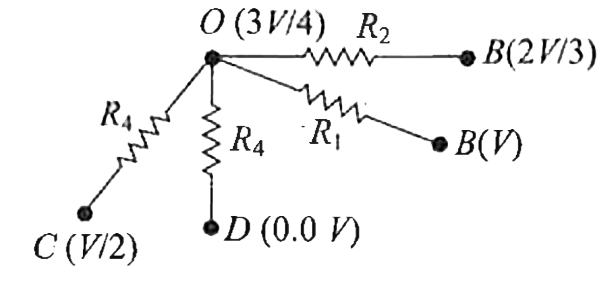 View Solution
View SolutionThe angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
View SolutionShow that 16R2rr1r2r3=a2b2c2
View SolutionA and B are two points on the parabola y2=4ax with vertex O. if OA is perpendicular to OB and they have lengths r1 and r2 respectively, then the valye of r4/31r4/32r2/31+r2/32 is
View SolutionIn an equilateral triangle with usual notations the value of 27r2Rr1r2r3is equal to
View SolutionIn ΔABC, if r=1,R=3,ands=5, then the value of a2+b2+c2 is _____
View SolutionIf r,r1,r2,r3 have their usual meanings , the value of 1r1+1r2+1r3, is
View SolutionThree circles with radius r1,r2,r3 touch one another externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 2. The value of (r1r2r3r1+r2+r3) is equal to
View Solution

