Assertion: A vector qunatity is a quantity that has both magnitude and a direction and obeys the triangle law of addition or equivalentyly the parallelogram law of addition.
Reason: The magnitude of the resultant vector of two given vectors can never be less than the magnitude of any of the given vector.
Resistance
Charge
Voltage
Current
The correct Answer is:D
To solve the given question, we need to analyze both the assertion and the reason provided.
Step 1: Analyze the Assertion
The assertion states that "A vector quantity is a quantity that has both magnitude and a direction and obeys the triangle law of addition or equivalently the parallelogram law of addition."
- Explanation:
- A vector quantity indeed has both magnitude (how much) and direction (which way).
- The triangle law of vector addition states that if two vectors are represented as two sides of a triangle taken in order, then their resultant is represented by the third side of the triangle taken in the opposite order.
- The parallelogram law states that if two vectors are represented in magnitude and direction by two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal of the parallelogram that passes through the point of intersection of the two sides.
- Conclusion: The assertion is true.
Step 2: Analyze the Reason
The reason states that "The magnitude of the resultant vector of two given vectors can never be less than the magnitude of any of the given vectors."
- Explanation:
- This statement is incorrect. The magnitude of the resultant vector can indeed be less than the magnitude of either of the individual vectors.
- For example, if we have two vectors A and B acting in opposite directions (180 degrees apart), the resultant vector R can be calculated as:
R=|A|−|B|
If |A| is less than |B|, then R will be negative, indicating that the resultant vector's magnitude is less than that of vector B.
- Conclusion: The reason is false.
Final Conclusion
- The assertion is true, while the reason is false. Therefore, the correct answer is that the assertion is true, and the reason is false.
---
The assertion states that "A vector quantity is a quantity that has both magnitude and a direction and obeys the triangle law of addition or equivalently the parallelogram law of addition."
- A vector quantity indeed has both magnitude (how much) and direction (which way).
- The triangle law of vector addition states that if two vectors are represented as two sides of a triangle taken in order, then their resultant is represented by the third side of the triangle taken in the opposite order.
- The parallelogram law states that if two vectors are represented in magnitude and direction by two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal of the parallelogram that passes through the point of intersection of the two sides.
The reason states that "The magnitude of the resultant vector of two given vectors can never be less than the magnitude of any of the given vectors."
- This statement is incorrect. The magnitude of the resultant vector can indeed be less than the magnitude of either of the individual vectors.
- For example, if we have two vectors A and B acting in opposite directions (180 degrees apart), the resultant vector R can be calculated as:
R=|A|−|B|
If |A| is less than |B|, then R will be negative, indicating that the resultant vector's magnitude is less than that of vector B.
- The assertion is true, while the reason is false. Therefore, the correct answer is that the assertion is true, and the reason is false.
Topper's Solved these Questions
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Exercise-01
Explore 24 Videos
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Exercise-02
Explore 53 Videos
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:EXERCISE-5(A)
Explore 15 Videos
- AIIMS 2019Book:ALLENChapter:AIIMS 2019Exercise:PHYSICS
Explore 40 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (J-A)
Explore 6 Videos
Similar Questions
Find the magnitude and direction of the resultant of given vectors
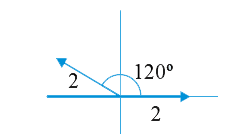
View SolutionState parallelogram of law of vector addition .
View SolutionA quantity has magnitude and direction .can you call it a vector ?
View SolutionState triangle law of of vector addition .
View SolutionThe magnitude of resultant vectors of two vectors given by →A=10ˆi+15ˆj and →B=5ˆi would be
View SolutionFind the magnitude and direction of the resultant of two vectors A and B in the terms of their magnitudes and angle θ between them.

View SolutionParallelogram law of vectors is applicable to the addition of :
View SolutionIf magnitude of the resultant of two vectors equal of magnitude, is equal to the magnitude of either of the vectors, what is the angle between them ?
View SolutionCan we have physical quantities having magnitude and direction which are not vectors?
View SolutionTwo vectors 3 units and 5 units are acting at 60∘ to each other .What is the magnitude and direction of the resultant ?
View Solution