α and β are the angle made by a vector from positive x & positive y-axes redpectively. Which set of α and β is not possible
[M−3L−1T3Q4]
[M−3L−2T4Q4]
[M−2L−2T4Q4]
[M−3L−2T4Q]
The correct Answer is:B
Step by step video & image solution for alpha and beta are the angle made by a vector from positive x & positive y-axes redpectively. Which set of alpha and beta is not possible by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exercise-01
24 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exercise-02
53 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-5(A)
15 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
α2,β2,γ2 are the angle which a line makes with positive x,y,z axes respectively. What is the value of cosα+cosβ+cosγ? (A) 1 (B) −1 (C) 2 (D) 3
View SolutionConsider the family of planes x+y+z=c where c is a parameter intersecting the coordinate axes P, Q andR and α,βandγ are the angles made by each member of this family with positive x, y and z-axes. Which of the following interpretations hold good got this family?
View SolutionIf α,βandγ are angles made by the line with positive direction of X-axis, Y-axis and Z-axis respectively, then find the value of cos2α+cos2β+cos2γ.
View SolutionIf α,β,γ be the angles which a line makes with the coordinates axes, then
View SolutionVector →P angle α,β and γ with the x,y and z axes respectively.
Then sin2α+sin2β+sin2γ=
View SolutionThe vector →a=αˆi+2ˆj+βˆk lies in the plane of the vectors →b=ˆi+ˆj and →c=ˆj+ˆk and bisects the angle between →b and →c . Then which one of the following gives possible values of α and β ? (1) α=2,β=2 (2) α=1,β=2 (3) α=2,β=1 (4) α=1,β=1
View SolutionIf α,β,γ are the angles which a line makes with positive direction of the axes, then match the quantities in column-I to their values in column-II:
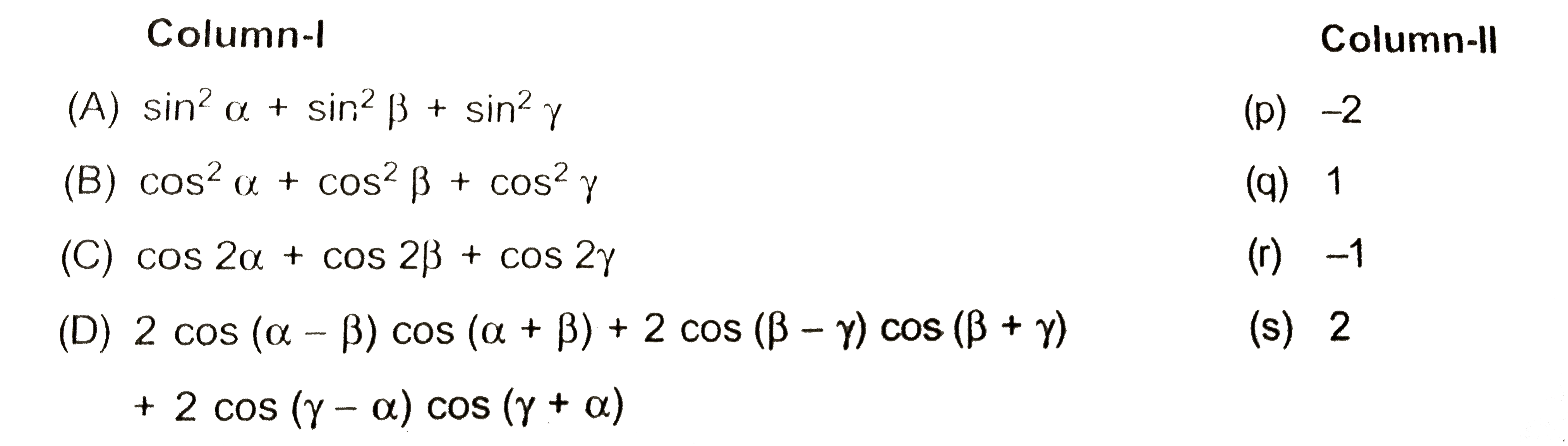
View SolutionIf αandβ are acute angles and sinα=35,sinβ=817, find the values of sin(α+β),cos(α±β),andtan(α±β).
View Solutionαandβ are acute angles and cos2α=3cos2β−13−cos2β then tanαcotβ=
View SolutionThe vector →a=αˆi+2ˆj+βˆk lies in the plane of the vectors →b=ˆi+ˆj and →c=ˆj+ˆk and bisects the angle between →b and →c . Then which one of the following gives possible values of αandβ ? (1) α=2,β=2 (2) α=1,β=2 (3) α=2,β=1 (4) α=1,β=1
View Solution
