The area of a circle is given by A=πr2, where r is the radius . Calculate the rate of increases of area w.r.t. radius.
Text Solution
The correct Answer is:20√ln2
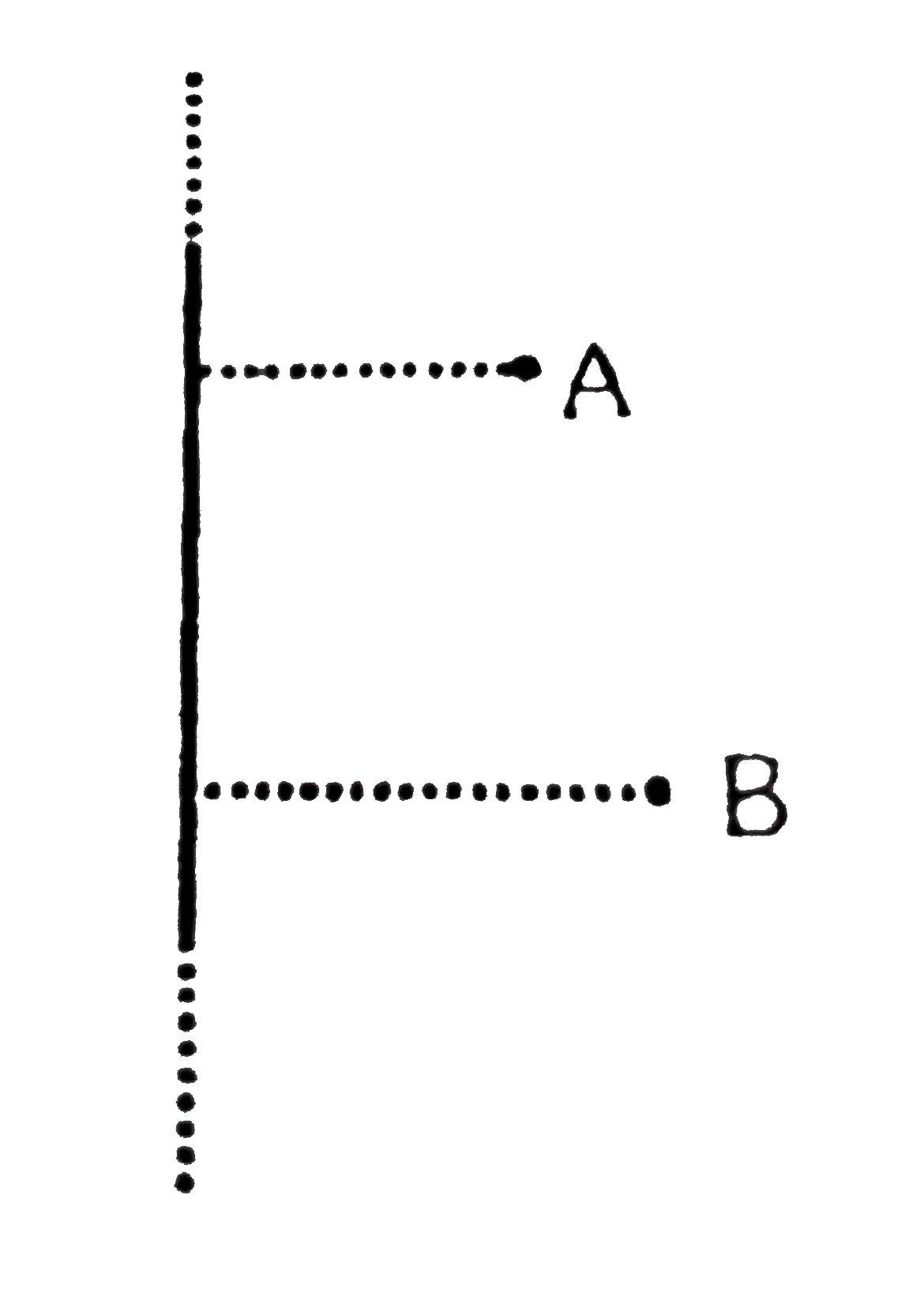
Force at Aλq2π∈0r=100
λq2π∈0×0.2=100B∫Adv=−B∫A→E.dr
VB−VA=−λ2π∈0r2∫r1drr=−λ2π∈0lnr2r1
VA−VB=λ2π∈0lnr2r1=λ2π∈0ln2
COME: KA+UA=KB+UB
0+λQ2π□∈0ln2=12mv2,20ln2=12×0.1×V2
V=20√ln2
|
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - PHY
68 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-3
20 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Comprehension 9
2 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Knowledge Check
If the rate of increase of the radius of a circle is 5 cm/sec, then the rate of increase of its area, when the radius is 20 cm, will be
A10πB20πC200πD400πIf the radius of a circle increases at a uniform rate of 2cm/s, then the rate of increase of area of circle, at the instant when the radius is 20 cm, is
A80πm2/sB80m2/sC80πcm2/sD80cm2/sThe area of a sector of angle θ∘ of a circle with radius R is
A2πRθ180BπR2θ180C2πRθ360DπR2θ360
If radius of circle if 4r, the area of circle is equal to :
View SolutionIf the radius of a circle is tripled, what is the ratio of the area of half the original circle to the area of the whole new circle? (Area of a circle =πr2, where r = radius)
View SolutionIf V denotes the volume and S is the surface area of a sphere. If radius of sphere is 2 cm, then the rate of change of V w.r.t. S is
View SolutionIf the radius of a circle be increasing at a uniform rate of 2cms−1. The rate of increasing of area of circle, at the instant when the radius is 20 cm is
View SolutionThe rate of change of surface area of a sphere of radius r when the radius is increasing at the rate of 2 cm/sec is proportional to
View Solution
