The area of a blot of ink is growing such that after t seconds, its area is given by A=(3t2+7)cm2. Calculate the rate of increase of area at t=5 second.
The correct Answer is:(i) 4a,(5a,0) (ii) V=Q4π∈0(13a−x−23a+x) for x≤3a,Q4π∈0(1x−3a−23a+x) for x>3a
(iii) √Qq8π∈0ma
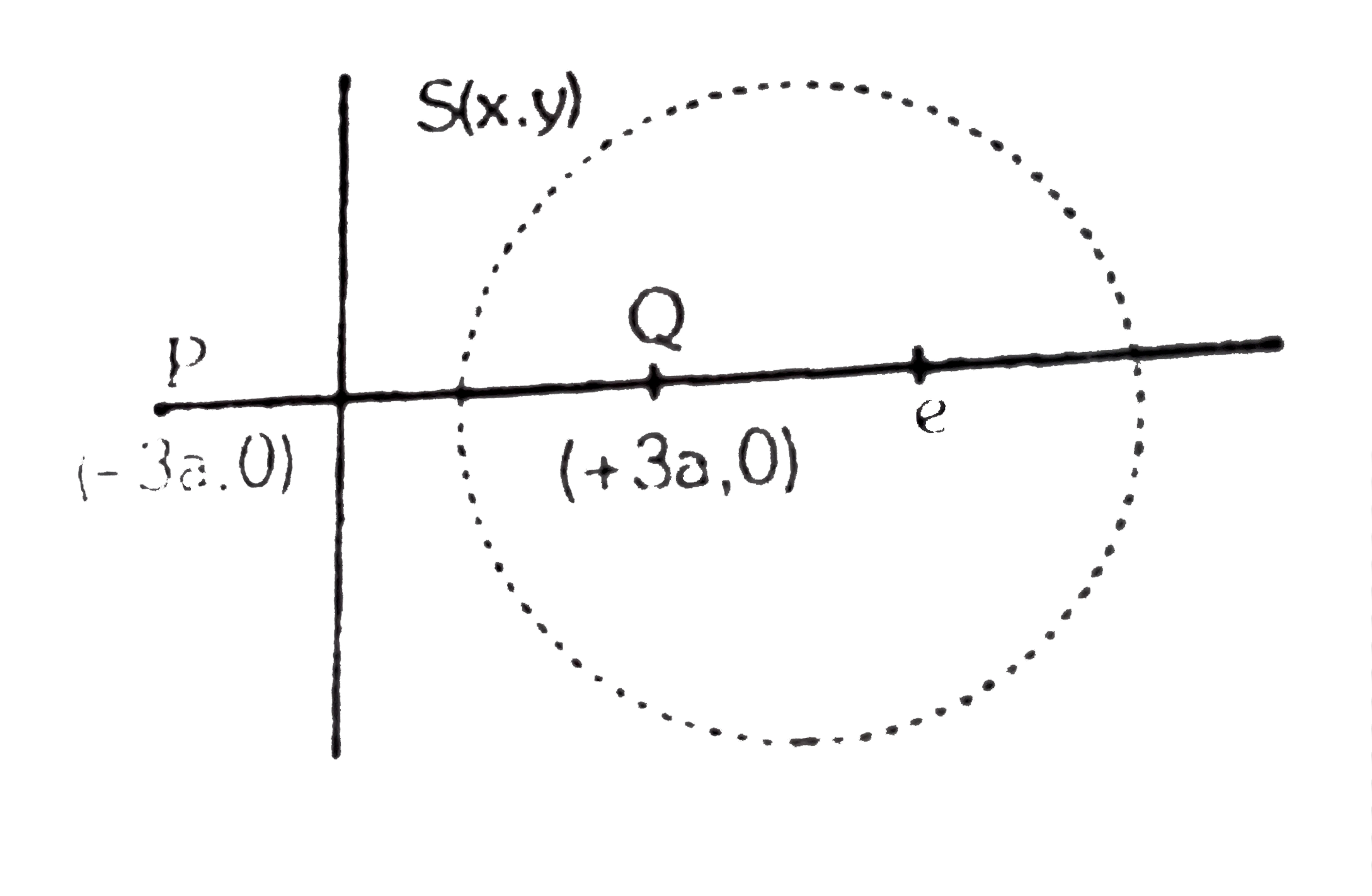
[A]VS=0=KQ√(x−3a)2+y2−2KQ√(x+3a)2+y2
⇒(x−5a)2+y2=(4a)2∴C=(5a,0) and radius =4a
[B]V(x)=KQx−3a−2KQx+3a for x>3a
=KQ(3a−x)−2KQ3a+x for x<3a
[C] A positive charge when released will move from high potential to low potential
COME: K1+U1=K2+U2
0+q[KQ2a−2KQ8a]=12mv2+0⇒V=√Qq8π∈0ma
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - PHY68videos
BASIC MATHS
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-320videos
BASIC MATHS
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Comprehension 92videos
BASIC MATHS
- BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS40videos
AIIMS 2019
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
Similar Questions
The area of dot of ink in cm2 is growing such that after 5s , A=3t2+(t/5)+7 .Calculate the rate of increase of area after 5s.
View SolutionA metallic disc is being heated. Its area (in m2) at any time t (in sec) is given by A=5t2+4t. Calculate the rate of increase in area at t=3sec.
View SolutionThe area of a circle is given by A=πr2, where r is the radius. Calculate the rate of increase of area w.r.t radius.
View SolutionA metallic disc is being heated. Its area A(in m2) at any time t(in second) is given by A=5t2+4t+8. Calculate the rate of increase in area at t=3s.
View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View SolutionA particle starts moving and its displace-ment after t seconds is given in meter by the relation x=5+4t+3t2. Calculate the magnitude of its
a. Initial velocity
b. Velocity at t=3s
c. AccelerationView SolutionA particle starts from origin with uniform acceleration. Its displacement after t seconds is given in meter by the relation x=2+5t+7t2. Calculate the magnitude of its
a. Initial velocity
b. Velocity at t=4s
c. Uniform acceleration
d. Displacement at t=5sView SolutionElectric current in a wire is time rate of flow of charge. The charge in coulombs that passes through a wire after t seconds is given by the function q(t)=t2−2t2+5t+2. Determine the average current (in coulmbe per second) during the first two seconds.
View SolutionThe velocity of a particle is given by v=(2t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=2 second.
View SolutionThe velocity of a particle is given by v=(4t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=1 second.
View Solution

